全国公立高校入試 　１番問題　【令和２年春】	正　答　６
	41　佐賀県　〜　47　沖縄県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

41佐賀県	１ (1) −11　　(2) 6×(−)＝−9 　(3) 　2(2x＋3y)−（x＋5y) ＝ 3x＋y 　2 2 　(4) 3−2√3−3＝−2√3 ２ (x＋12)(x−3) ３ 単位に注意 　a−b＜2 ４ 球の半径は,2cmとなるから, 　体積＝×π×23＝32/3πcm3 ５ 解の公式より, 　x＝ −3±√32−4×1×(−1) 2×1 　　＝ −3±√9＋4 ＝ −3±√13 2 2 ６ 対角は等しいから,∠B＝70° 　∠x＝42＋70＝112° ７ 各値を計算すると, Aｸﾞﾙｰﾌﾟ Bｸﾞﾙｰﾌﾟ 正誤 �@ 70 ＞ 50 〇 �A 70 ＞ 50 × �B 0.2 ＜ 0.3 × �C 7 ＞ 4 〇 　よって,�@�C	44熊本県	１ 660　　２ 6＋9＝15 ３ 　（9x＋5y）−4(x−y) ＝ 9x＋5y−4x＋4y 　8 8 　＝ 5x＋9y 8 ４ 　8a3b2 ＋ 4a2b2 ＝2a＋1 　4a2b2 4a2b2 ５ 9x2−49−9x2＋9x＝9x−49 ６　5＋2√5＋1−3√5＝6−√5 　〜２番問題の一部（おまけ）〜 １ −4x＝20より,x＝−5 ２ 解の公式より, 　x＝ −(−3)±√(−3)2−4×1×(−1) 2×1 　　＝ 3±√9＋4 ＝ 3±√13 2 2 ３ ア,イ,エ （アはy＝x2 イはy＝360/x エはy＝0.03x）
42長崎県	【　Ａ　】 １ 6−8＝−2 ２ 　6−5 ＝ 　10 ３ 3√5−4√5＝−√5 ４ 980×1.1＝1078円 ５ 3a＋4b＜3000 ６ 共通因数（x＋y）でくくりだすと, 　(a＋2)(x＋y) ７ 解の公式より, 　x＝ −(−3)±√(−3)2−4×1×(−2) 2×1 　　＝ 3±√9＋8 ＝ 3±√17 2 2 ８ ∠O(xの反対側の中心角) 　　＝110×2＝220° よって,∠x＝360−220＝140° ９ 白玉をx個とすると、 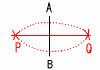　白玉の比率＝ 　x . ＝ 6 より､ 500 30 　x＝500×6÷30＝100個 10 右図 ・AとBから,AP＝BPと 　　なる弧をかく ・AとBから,AQ＝BQと 　　なる弧をかく ・PとQを通る直線をかく	45宮崎県	１ −17 ２ ×(−)＝− ３ 2a＋8b＋3a−7b＝5a＋b ４ √24÷√6＝√4＝2 ５ 下式より,x＝4y−1 　これを上式に代入すると, 　　2(4y−1)＋3y＝20 　　8y−2＋3y＝20より,11y＝22で,y＝2 　これを下式に代入して,8＝x＋1より,x＝7 　よって,x＝7,y＝2 ６ 解の公式より, 　x＝ −(−1)±√(−1)2−4×3×(−1) 2×3 　　＝ 1±√1＋12 ＝ 1±√13 6 6 ７ (ならない確率)＝1−(なる確率) 　和が8となるのは,次の5通り 　　2＋6, 3＋5, 4＋4, 5＋3, 6＋2 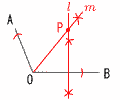よって,確率＝1− 　5 . ＝1− 5 ＝ 31 6×6 36 36 ８　右図 ・∠AOBの二等分線l を引く ・線分OBの垂直二等分線m 　　　を引く ・l とmの交点をPとする
	【　Ｂ　】 １ 2−2√2＋1−5√2＋ 14√2 √2√2 　＝3−7√2＋7√2＝3 ２ 3a＋4b＜3000 ３ x＋y＝Ａとおくと, 　与式＝A2＋7A＋12＝(A＋3)(A＋4) 　　＝(x＋y＋3)(x＋y＋4) ４ x2＋x−6＋2x＝0 　x2＋3x−6＝0 解の公式より, 　x＝ −3±√32−4×1×(−6) 2×1 　　＝ −3±√9＋24 ＝ −3±√33 2 2 ５ 赤玉をx個とすると、 　白玉の比率＝ 　x　 . ＝ 20−4 より､ x＋100 20 　20x＝16(x＋100)で、x＝400個 ６ nの因子に,2が0個または2個 2が0個…1, 5,101,5×101 で4個 2が2個…22,22×5,22×101, 　22×5×101 で4個 よって,4＋4＝8個 ７ ∠O(xの反対側の中心角) 　　＝110×2＝220° よって,∠x＝360−220＝140° 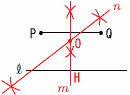８ 右図 ・線分PQの垂直 　二等分線mを引く ・l とmの交点Hをとる ・線分PHの垂直 　二等分線nを引く ・mとnの交点Ｏをかく	46鹿児島県	１ (1) 2＋6＝8 　(2) ＋＝2 　(3) 2√3＋3√3−√3＝4√3 　(4) エ 　ab＜0より,aとbは異符号 　ab＜0の両辺にcをかけると,不等号の向きが 　　逆になることより,c＜0 　(5) ア　(平面図は手前がとがっている) ２ y＝に(2,−3)を代入すると, 　　−3＝a/2で,a＝−6 　よって,y＝− ３ √7＜x＜√31より, 　　各辺を2乗して,7＜x2＜31 　xは整数だから, x＝3,4,5 ４ 1,2,…,6 を1つの群〇と考えると, 　　100÷6＝16余り4 　つまり, 〇〇〇〇〇〇,1,2,3,4 だから, 4 ５ 1.5x＞1936より,x＞1936÷1.5 　x＞1936×＝1290.66…で, イウキ
43大分県	１ (1) −4　(2) −3×(−4)＝12 　(3) 　4a＋2b＋3a−3b ＝ 7a−b 　6 6 　(4) 　xy2×x2 ＝x2y 　xy 　(5) 　　6√3 . ＋√3√5×√5 　√3√3 　　＝2√3＋5√3＝7√3 ２ (x＋9)(x−2)＝0より,x＝−9,2 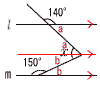３ (右図参照) 　∠xを平行線で2分すると, 　　平行線上の 　　　錯角が等しいから 　　a＝180−140＝40° 　　b＝180−150＝30° 　∠x＝a＋b＝70° ４ a−3＝√5だから, 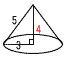　　2乗して,a2−6a＋9＝5 ５ (右図参照) 　円錐の高さは4cmだから, 　体積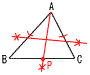＝×32π×4＝12πcm3 ６ 右図 　・∠Aの二等分線 　・BCとの交点をPとする 　・APの垂直二等分線が答	47沖縄県	１ −2　　２ 6×(−)＝−9　　３ 0.61 ４ √2＋3√2−4√2 ５ 4a×9a2＝36a3 　〜２番問題の一部（おまけ）〜 １ 2x＝8より,x＝4 ２ 下式×2−上式より、5y＝−5で、y＝−1 　これを下式に代入して、x＋3×(−1)＝3 　　x＝3＋3＝6 　よって、x＝6、y＝−1 ３ x2−3x−18 ４ (x＋6)(x−6) ５ 解の公式より, 　x＝ −5±√52−4×1×(−1) 2×1 　　＝ −5±√25＋4 ＝ −5±√29 2 2

［トップに戻る］　［前ページに戻る］