|
乮俀俋乯撧椙導 | 妛廗擔丂丂丂 寧丂丂 丂擔乮丂丂丂乯 |
|
乮俀俋乯撧椙導 | 妛廗擔丂丂丂 寧丂丂 丂擔乮丂丂丂乯 |
| 亂丂堦丂斒丂亃 | |||||||||||||||||||||||||||||
| 1 | (1) 丂 |
俈 | 丂師偺亂A亃,亂B亃偺暥復偼,妋棪偵偮偄偰弎傋偨傕偺偱偁傞丅
(1) p偺抣傪媮傔傛丅 (2) p偺抣偲q偺抣偺娭學偵偮偄偰惓偟偔弎傌偰偄傞傕偺傪,師偺傾乣僂偐傜侾偮慖傃,偦偺婰崋傪彂偗丅
|
||||||||||||||||||||||||||
| (2) 丂 |
|||||||||||||||||||||||||||||
| (3) (4a3b亄6ab2)亐2ab 丂丂丂丂丂丂丂 |
|||||||||||||||||||||||||||||
| (4) (x亄y)2亅5xy 丂 |
|||||||||||||||||||||||||||||
| 俀 | 丂愨懳抣偑4傛傝彫偝偄惍悢偼壗屄偁傞偐丅 |
||||||||||||||||||||||||||||
| 俁 | 丂2師曽掱幃 x2亄5x亄2亖0 傪夝偗丅 |
||||||||||||||||||||||||||||
| 係 |
|
俉 | 丂堦偺埵偺悢偑侽偱側偄2寘偺帺慠悢A偑偁傞丅A偺廫偺埵偺悢偲乕偺埵偺悢傪擖傟偐偊偰偱偒傞悢傪B偲偡傞丅 (1) A偺廫偺埵偺悢傪x,乕偺埵偺悢傪y偲偡傞偲偒,B傪x,y傪巊偭偨幃偱昞偣丅 (2) A偺廫偺埵偺悢偼堦偺埵偺悢偺2攞偱偁傝,B偼A傛傝36彫偝偄丅偙偺偲偒,A偺抣傪媮傔傛丅 丂 |
||||||||||||||||||||||||||
| 俆 | 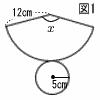 丂恾1偼,墌偡偄偺揥奐恾偱,掙柺偺敿宎偼5cm,懁柺偺偍偆偓宍偺敿宎偼12cm偱偁傞丅佢x偺戝偒偝傪媮傔傛丅 丂恾1偼,墌偡偄偺揥奐恾偱,掙柺偺敿宎偼5cm,懁柺偺偍偆偓宍偺敿宎偼12cm偱偁傞丅佢x偺戝偒偝傪媮傔傛丅 |
||||||||||||||||||||||||||||
| 俇 |
|
||||||||||||||||||||||||||||
| 亂丂摿怓慖敳丂亃 | ||||||||||
| 1 | (1) 丂 |
俆 | 丂2偮偺偝偄偙傠A,B傪摨帪偵搳偘傞偲偒,弌傞栚偺悢偺榓偑10埲忋偵側傞妋棪傪媮傔傛丅 丂 |
|||||||
| (2) 丂 |
||||||||||
| (3) 丂 |
俇 | 丂師偺帒椏偼,偁傞拞妛峑偺棨忋晹堳8恖偑斀暅墶偲傃傪20昩娫峴偭偨偲偒偺寢壥偱偁傞丅偙偺帒椏偵偍偗傞拞墰抣乮儊僕傾儞乯傪媮傔傛丅 丂
丂 |
||||||||
| (4) (x亅3)2亄(x亄1)(x亅3) 丂 |
||||||||||
| (5) 4併7亅併28 丂 |
俈 | 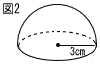 丂恾2偼,敿宎偑3cm偺敿媴偱偁傞丅偙偺敿媴偺懱愊傪媮傔傛丅偨偩偟,墌廃棪偼兾偲偡傞丅 丂恾2偼,敿宎偑3cm偺敿媴偱偁傞丅偙偺敿媴偺懱愊傪媮傔傛丅偨偩偟,墌廃棪偼兾偲偡傞丅丂 |
||||||||
| 俀 | 丂2師曽掱幃 x2亄x亅12亖0 傪夝偗丅 丂 |
|||||||||
| 俁 | 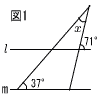 丂恾1偱,l //m偱偁傞偲偒,佢x偺戝偒偝傪媮傔傛丅 丂恾1偱,l //m偱偁傞偲偒,佢x偺戝偒偝傪媮傔傛丅丂 |
俉 | 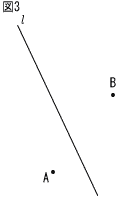 丂恾3偺傛偆偵,捈慄 l偲2揰A,B偑偁傞丅師偺忦審嘆,嘇傪枮偨偡揰俹傪,掕婯偲僐儞僷僗傪巊偭偰夝摎棑偺榞撪偵嶌恾偣傛丅側偍,嶌恾偵巊偭偨慄偼徚偝偢偵巆偟偰偍偔偙偲丅 丂恾3偺傛偆偵,捈慄 l偲2揰A,B偑偁傞丅師偺忦審嘆,嘇傪枮偨偡揰俹傪,掕婯偲僐儞僷僗傪巊偭偰夝摎棑偺榞撪偵嶌恾偣傛丅側偍,嶌恾偵巊偭偨慄偼徚偝偢偵巆偟偰偍偔偙偲丅[忦審] 丂嘆 揰俹偼,捈慄 l忋偵偁傞丅 丂嘇 佢APB亖佢PBA偱偁傞丅 |
|||||||
| 係 | 丂2偮偺懳妏慄偺挿偝偑偦傟偧傟acm,bcm偱偁傞傂偟宍偺柺愊傪昞偟偨幃偑,師偺傾乣僆偺拞偵1偮偁傞丅偦偺幃傪慖傃,傾乣僆偺婰崋偱摎偊傛丅
|
|||||||||
| 乵僩僢僾偵栠傞乶 乵慜儁乕僕偵栠傞乶丂乵師儁亅僕偵恑傓乶 乵摎偺儁亅僕偵恑傓乶丂 |