|
���@���@�R | |||
| 17�@�ΐ쌧�@�`�@24�@�O�d�� |
|
���@���@�R | |||
| 17�@�ΐ쌧�@�`�@24�@�O�d�� |
�` ������āA���̏�ł���ăl�I �i�����T�C�Y�����ɂ���Ƃ`�S�Ɏ��܂�܂��j�`
| 17�ΐ쌧 | �P (1) 5�{2��7 �@(2) �|2�~9�{4���|18�{4���|14
�Q ���̌������,
(��,��)��(1,5) (5,1) (2,5) (5,3) (3,5) �@(5,3) (4,5) (5,4) (5,5) (5,6) (6,5) �����,�m����11��62��11/36 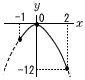 �S(�E�}�Q��) �S(�E�}�Q��)�ŏ��l��,x��2�̂Ƃ���, y���|12������, �@a�~22���|12��,a���|3 �T 10�l�̒����l��5�Ԗڂ�6�Ԗ� �@��2�l�̕��ϒl��25��,����4����, �@�@5�Ԗڂ�23��,6�Ԃ�27�� 11�l�̒����l��6�Ԃ�,27�� |
22���� | �P (1) �|12�{3���|9
�Q �^����a(b�{9)(b�|9)�� �R x�{1���}��3���,x���|1�}��3 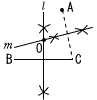 �@�`�Q�Ԗ��i���܂��j�` �@�`�Q�Ԗ��i���܂��j�`�P �E�} �EBC�̐�������l ������ �EAC�̐�������m������ �El ��m�̌�_��O�Ƃ��� �@�iAC�̑����AB�ł��j �Q �d��y�͒���x�ɔ�Ⴗ�邩��,y��ax�Ƃ�,
�R (���Ȃ��Ƃ�1��3�̔{���̊m��) �@��1�|(2�Ƃ�3�̔{���łȂ��m��)
|
||||||||||||||||||||||||||||||||||||||||||
| 18���䌧 | AB�P (1) 7�{8��15�@(2) 4��2�|��2��3��2
A�Q (x�|4)(x�|7) A�RB�Q x�{1���}��5���,x���|1�}��5 A�SB�R �@�̓A,�A�̓G A�TB�S �O�p�̘a��360��������, ��x��360�|40�{90�{100�{60)��70�� B�T �䗦�ɂ�萄�肷��
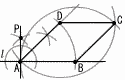 AB�U �E�} �El �̐���PA������ �E��PAB�̓��������� �EAB��AD�ƂȂ�_D���Ƃ� �EAB��BC��DC�ƂȂ�_C���Ƃ� |
23���m�� | �@�y�@�`�@�z �P 8�|(�|3)��8�{3��11
���̌������,
�V x��4�̂Ƃ�,y�� �@x��6�̂Ƃ�,y��
�X AB:DC��6:4��3:2���,AE:CE��3:2 ��ABC�䁢EFC������,AB:EF��AC:EC�� �@6:EF��(3�{2):2���,EF��6�~2��5�� |
||||||||||||||||||||||||||||||||||||||||||
| 19�R���� |
�@�`�Q�Ԗ��i���܂��j�` �P �������㎮�ɑ������, �@2(3y�{2)�|5y��6 �@6y�|5y��6�|4��,y��2 ����������ɑ������,x��3�~2�{2��8 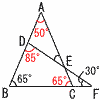 �����,x��8,y��2 �����,x��8,y��2�Q(�E�}�Q�Ɓj ��A��180�|65�~2��50�� ��BDF��180�|65�|30��85�� ��DEA��85�|50��35�� �R y��800/x (�����)��,�E (�Q�l)���̎��͎��̒ʂ� �@�A y��20�|x (1����) �@�C y��4��x3 (3��ɔ��) �@�G y��3x (���) �S 5����2���o�����@�͑S����, �@5�~4��2��10�ʂ� ��(R1,R2,R3),��(B)��4����1�� �@��1�����o�����@��,4�~1��4�ʂ� �����,�m����4/10�� �T ������Ⴂ���ɕ��ׂ��, �@26,27,30,34,34,35,35,35,37,37 (1) �����l��(34�{35)��2��34.5�� (2) 34����2��,35����3��������,
|
�@�y�@�a�@�z
�S 1���̒艿��x�~�Ƃ����, 0.7x�~2��2000�|880��,1.4x��1120 �@x��1120��1.4��800�~ �T �|x�{2��2x�|7���,�|3x���|9��,x��3 �@�܂�,y���|3�{2���|1 �����,��_��(3,�|1) �U �e�ӂ�2�悵��, �@67.24��n�{1��70.56 �@n�{1��68,69,70���,n��67,68,69 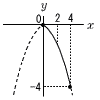 �V(�E�}�Q��) �V(�E�}�Q��)�ő�l��0������,a��0 �@(�O���t�͏�ɓ�) x��4�̂Ƃ�,y���|4��, �@�|4��a�~42 �@16a���|4���,a���| �W a�|b��2�ƂȂ�̂�, �@(a,b)��(3,1) (4,2) (5,3)��3�ʂ� ���ׂẴJ�[�h�̎��o������ 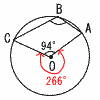 �@5�~4��20�ʂ� �@5�~4��20�ʂ������,�m����3/20 �X(�E�}�Q��) �傫�����̒��S�p �@��AOC��360�|94��266�� �~���p��,��B��266��2��133�� |
|||||||||||||||||||||||||||||||||||||||||||
| 20���쌧 | �P �|2�@�@�Q �S ��C����B��68��,��ADC��90�����, ��x��180�|90�|68��22�� �T �ڍ�����,2x2�{3x�|1��0 ���̌������,
�U �^����5x�|y�|2x�{6y��3x�{5y
�V 5�����瓯����2�����o�����@�͑S����, �@5�~4��2��10�ʂ� �a��3�ɂȂ�̂�,(0,3)(1,2)(2,4)��3�ʂ� �����,�m���� �W y���| �X �䗦���琄�肷��
10 a2�{b2��c2�Ȃ�Β��p�O�p�` |
24�O�d�� | �@�y�@�`�@�z �P �|18��9���|2 �Q 4x�|4�{3x�|6��7x�|10
�S �A����������������,��_�����߂�
�@�|1��6a�{1���,a���| �T 5�|5��5�|14�|��5���|9�|6��5 �U x2�|3x�|10�{10��0 �@x(x�|3)��0���,x��0,3 �V ���Ƃ���,a��1,b���|2�Ƃ����, �|a���|1,�|b��2,a�|b��3,b�|a���|3 �����, b�|a, b, �|a, a, �|b, a�|b �W A�g��x�l�Ƃ����,B�g��(70�|x)�l �@81x�{88(70�|x)��84.4�~70 �@81x�|88x��5908�|6160 �@�|7x���|252���,x��36�l 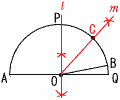 �X �E�} �X �E�} ��BOC��45���ɂȂ�悢 �EAO�̐��� l ������ �E��POQ�̓���m������ �E��AB��m�̌�_��C�Ƃ��� |
||||||||||||||||||||||||||||||||||||||||||
| 21�� | �P 10�|16���|6 �Q 8a�{4b�|2a�{6b��6a�{10b �R �^����(x�|3)2��(��2�|3�{3)��(��2)2��2 �S �䗦���琄�肷��
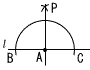 x��27�~47��3��423��,��420�C x��27�~47��3��423��,��420�C�T �A,�G �U �E�} �EA����AB��AC�ƂȂ�_B,C���Ƃ� �EB��C����,BP��CP�ƂȂ�_P���Ƃ� �P��A������ �@�`�Q�Ԗ��i���܂��j�` �P y��ax2��(�|1,2)��������, �@(�|1)2a��2���,a��2 �Q y��2x2��x��2��������,y��2�~22��8 �@B�̍��W��(2,8) l ��y��px�{q�Ƃ���,A��B�̍��W���������,
�R ��AOB����AOC�{��BOC(OC����) �� �@�`�R�Ԗ��i���܂��j�` �P ( �Q �Ԕ��Ƃ��� �R (��1,��2)��(��2,��1)������,
|
�@�y�@�a�@�z �P �|5 �Q �R 3a�{6b�|2a�{b��a�{7b �S (��7)2�|(2��5)2��7�|20���|13 �T (x�|6)(x�{5) �U ���̌������,
�V ���o��������x�Ƃ����,�Ԃ�2x�� �@(45�|2x):(27�|x)��7:5���, �@7(27�|x)��5(45�|2x) �@189�|7x��225�|10��x �@10x�|7x��225�|189 �@�@�@3x��36��,�@x��12�� �@ |
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |