全国公立高校入試 　１番問題　【平成３１年春】	正　答　２
	９　栃木県　〜　16　富山県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

９栃木県	１ −2 ２ 2(3x−2)＝6x−4 ３  5ab2×3 ＝15b2  a ４ x2＋2x−48 ５ ±5 ６ 多角形の外角の和は360°だから, ∠x＝360−(60＋90＋35＋105)＝70° ７ y＝ に(6,−2)を代入して,−2＝  a  6 a＝−2×6＝−12 ８ 面積比は相似比の2乗だから, 8:△DEF＝22:32より, 　△DEF＝8×9÷4＝18cm2 ９ 上式×3−下式より,7x＝−21で,x＝−3 これを上式に代入して,−9＋y＝−5で,y＝4 よって,x＝−3,y＝4 10 6/36＝ 11 ∠BOC＝360-248＝112° よって,∠x＝112÷2＝56° 12 解の公式より, 　x＝ −7±√72−4×1×1 2×1 　　＝ −7±√45 ＝ −7±3√5 2 2  13 式はy＝150−2xで,ウ 14 ア	13東京都	１ 5−4＝1 ２ 4a−4b−a＋9b＝3a＋5b ３ 7−2√7＋1＝8−2√7 ４ 移項して,4x−5x＝15−6 　−x＝9より,x＝−9 ５ 上式×3＋下式より,5y＝30で,y＝6 これを下式に代入して,3x−6＝6で,x＝4 よって,x＝4,y＝6 ６ 解の公式より, 　x＝ −1±√12−4×1×(−9) 2×1 　　＝ −1±√1＋36 ＝ −1±√37 2 2  ７ カードの取り出し方は全部で 　5×4÷2＝10通り 積が3の倍数となるのは,次の6通り 　(1,2,3,) (1,3,4) (1,3,5) 　(2,3,4) (2,3,5) (3,4,5) 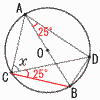よって,確率＝6/10＝ ８(右図参照) ∠BCD＝∠BAD＝25° ∠ACB＝90°より, 　∠x＝90−25＝65° ９ 右図 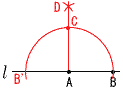・Ａを中心に, 　半径ABの円をかく ･ＢとB'から,BD＝B'Dと 　なる点をとる ・ADと円Aの交点をCとする
10群馬県	【前期】 １ (1) −4　(2) 3x　(3) 2(3a−1)＝6a−2 　(4) 4x＋5y−x−3y＝3x＋2y　(5) 2a2 　(6) 5√2−2√2＝3√2 ２ 2x2＋5x−3 ３ (x＋3y)(x−3y) 　〜２番問題（おまけ）〜 １ 2a＋3b＝500 ２ △BCFを底面と考えると, 体積＝(×4×4)×6＝16cm3 ３ x2−2x＋1−x−4＝0 整理して,x2−3x−3＝0 解の公式より, 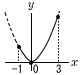　x＝ −(−3)±√(−3)2−4×1×(−3) 2×1 　　＝ 3±√9＋12 ＝ 3±√21 2 2 ４(右図参照) x＝3のとき,y＝32＝9 x＝0のとき,y＝02＝0 よって,0≦y≦9	14神奈川県	１ −20 (答１) ２  −21＋15 ＝−  6  (答２)  5×7 35 ３ −8ab (答３) ４ 3√7＋ 　42√7 ＝3√7＋6√7 √7√7 　＝9√7 (答２) ５ x2＋8x＋16−(x2−9x＋20) 　＝17x−4 (答４) 　〜２番問題（おまけ）〜 １ x−4＝Aとおくと,与式＝A2＋8A−33 　＝(A−3)(A＋11)＝(x−4−3)(x−4＋11) 　＝(x−7)(x＋7) (答１) ２ 解の公式より, 　x＝ −(−4)±√(−4)2−×3×2 3 　　＝ 4±√16−6 ＝ 4±√10  (答２) 3 3 ３ x＝0のとき,最大値b＝0 x＝−3のとき,a＝−×(−3)2＝−6 (答１) ４ 3割引きでは倍で,(2a＋b)＜5000 (答４) ５ 3数を2乗すると,75,64,79だから 　8＜5√3＜√79　(答３) ６ 不良品の比率が等しいと考えて, 比率＝ 　6 . ＝ 　 x　. より,  500 30000 x＝6×30000÷500＝360個　(答３)
	【後期】 １ (1) −12　(2) 3a3 (3)  2(x＋y)＋(x−y) ＝ 3x＋y  4 4 ２ 各辺を2乗して,4＜a＜9 よって,a＝5,6,7,8 ３ (x＋6)(x−1) 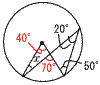４ 与式＝ −a3b3 ＝−a2b ab2  ＝−32×(−4)＝36 ５ x(x−6)＝0より,x＝0,6 ６（右図参照） ∠x＝(20＋50)−(20×2)＝30° ７ 4枚の硬貨をA,B,C,Dとする 表裏の出方は全部で,24＝16通り 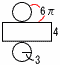表2枚の組合せは,次の6通り 　AB,AC,AD,BC,BD,CD よって,確率＝6/16＝ ８(右図参照)円周は6π 表面積＝底面積(円)×2＋側面積(長方形) 　＝32π×2＋4×6π＝42πcm2 ９ イ,エ
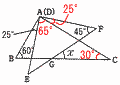
11埼玉県	１ 3a ２ 2−1＝1 ３  3x2×2xy3 ＝−6x3y −y2 ４ 　10√5 . −√9√5＝2√5−3√5＝−√5  √5√5 ５ (x＋9)(x−3) ６ 上式を下式に代入して, x−2(5−3x)＝4より,7x＝14で,x＝2 これを上式に代入して,y＝5−6＝−1 よって,x＝2,y＝−1 ７ 解の公式より, 　x＝ −(−3)±√(−3)2−4×2×(−1) 2×2 　　＝ 3±√9＋8 ＝ 3±√17 4 4 ８ y＝ax＋bに,(4,3)と(-2,0)を代入して, 　{ 4a＋b＝3 −2a＋b＝0 これを解いて,a＝ ,b＝1 よって,y＝ x＋1 ９(右上図参照) △ABCで,∠EAC＝90−25＝65° △AEFで,∠CAF＝90−65＝25° △ABCで,∠C＝180−90−60＝30° よって,∠x＝25＋45−30＝40° 10 イとエ 11 (1) 赤い布をa枚使うとすると, 45a＋5＝500より,a＝11枚 (2) 45x＋25y＋5＝500より, 9x＋5y＝99(1≦x≦10) x＝1,2,3,…,10を順に代入して, 　整数解を求めると,(x,y)＝(1,18),(6,9) (赤布,白布)＝(1枚,18枚),(6枚,9枚)	15新潟県	１ 4−18＝−14 ２ 2a＋4b−3a＋4b＝−a＋8b ３  a6b5×b3 ＝a4b8 a2 ４ 上式×3＋下式より,7x＝14で,x＝2 これを上式に代入して,2＋3y＝−1で,y＝−1 よって,x＝2,y＝−1 ５ 3√5＋√5＝4√5 ６ x(x＋7)＝0より,x＝0,−7 ７ 変化の割合＝ 52a−12a ＝6a＝−12 5−1  よって,a＝−2 ８ 底面の半径＝√132−122＝5cm 体積＝ ×52π×12＝100πcm3 ９ ∠BDC＝90−58＝32° ∠BOC＝32×2＝64° ∠x＋32＝24＋64より,∠x＝56° 10 グラフより,下の表にまとめる 階級値(cm) 42 46 50 54 58 62 66 計 度　数 (人) 3 4 6 9 5 2 1 30 階級値×度数 126 184 300 486 290 124 66 1576 平均値＝1576÷30＝52.5333≒52.5cm
12千葉県	【前期】 １ −5 ２ 7＋×4＝7＋3＝10 ３ 7x＋y−2x−3y＝5x−2y ４ 3b＝2−9aより, b＝ 2−9a または,b＝ −3a 3 ５ 　4√2 . −√18＝2√2−3√2＝−√2 √2√2 ６ 解の公式より, 　x＝ −1±√12−4×2×(−4) 2×2 　　＝ −1±√1＋32 ＝ −1±√33 4 4 【後期】 １ 12＋6＝18 ２ −25×＝−2 ３ 6a＋3b−4a− b＝2a＋ b ４ 下式×2−上式×3より, 　19y＝−57で,y＝−3 これを上式に代入して,2x＋9＝17で,x＝4 よって,x＝4,y＝−3 ５ 7−3√21＋6＝13−3√21 ６ 与式＝x2＋x−12−8＝x2＋x−20 　＝(x−4)(x＋5)	16富山県	１ 8−6＝2 ２ 9a＋1−6a＋4＝3a＋5 ３ −48x3y2÷12xy2＝−4x2 ４  　9√33 ＋2√3＝3√3＋2√3＝5√3  √3√3 ５ 3a＋5b＞500 ６ (x＋3)(x−2)＝0より,x＝−3,2 ７ 平行でない,かつ交わらない辺で, 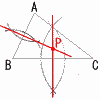CF,DF,EFの 3本 ８ 右図 △ABCの外心で,各辺の垂直二等分線の交点を作図すればよい。 ９(右図参照) 正五角形の1つの内角 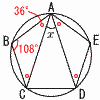　＝180×3÷5＝108° △ABCで,∠B＝108°, 　∠B＝∠C＝(180−108)÷2 　＝36° ∠x＝108−36×2＝36° 10 和が5となるのは 　(1,4) (2,3)の2通り 4個から2個取り出す方法は,4×3÷2＝6通り よって,確率＝2÷6＝