| １ |
 －2a＋5a
|
10 |
関数y＝x2について述べた次のア～オの中から,正しいものを2つ選び,その記号を書きなさい。
| ア |
この関数のグラフは,点(3,6)を通る。 |
イ
|
この関数のグラフは放物線で,y軸について対称である。 |
ウ
|
xの変域が－1≦x≦2のときのyの変域は1≦y≦4である。 |
エ
|
xの値が2から4まで増加するときの変化の割合は6である。 |
オ
|
x＜0の範囲では,xの値が増加するとき,yの値は増加する。 |
|
| ２ |
(－8)÷(－4)－1
|
| ３ |
3x2÷(－y2)×2xy3
|
| ４ |
|
11 |
次は,先生.Aさん,Bさんの会話です。これを読んで,下の(1),(2)に答えなさい。
先生
|
「縦20cm,横50cmの長方形の赤い布と縦20cm,横30cmの長方形の白い布を使って，縦20cm,横5mのゴールテープを作ろうと思います｡」 |
| Aさん |
「どのように作るのですか｡」 |
先生
|
「布は切らずに,ゴールテープの縦の長さは20cmにそろえて,横は布と布を5cmずつ重ねて縫い合わせます｡」 |
| Aさん |
「赤い布と白い布は何枚あるのですか｡」 |
| 先生 |
「どちらもたくさんあります｡」 |
Bさん
|
「Aさん,赤い布と白い布は横の長さが違うけれど,ちょうど5mにできるのかな｡」 |
| Aさん |
｢赤い布だけなら,[ア]枚使って5mにできるよ｡」 |
Bさん
|
「赤い布と白い布の両方を使って,ちょうど5mになる枚数の組はあるのかな｡」 |
| Aさん |
「どうだろう。考えてみよう｡」 |
(1) [ア]にあてはまる数を書きなさい｡
(2) 赤い布と白い布の両方を使って,ちょうど5mになる赤い布と白い布の枚数の組を,赤い布をx枚,白い布をy枚として,途中の説明も書いてすべて求めなさい。
|
| ５ |
x2＋6x－27を因数分解しなさい。
|
| ６ |
| 連立方程式 { |
y＝5－3x |
を解きなさい。 |
| x－2y＝4 |
|
| ７ |
2次方程式 2x2－3x－1＝0 を解きなさい。
|
| 8 |
yがxの1次関数で,そのグラフが2点(4,3),(－2,0)を通るとき,この1次関数の式を求めなさい。
|
| ９ |
図1のような.1組の三角定規があります。この1組の三角定規を,図2のように,頂点Aと頂点Dが重な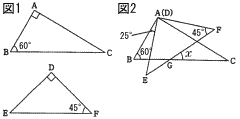 るように置き,辺BCと辺EFとの交点をGとします。∠BAE=25°のとき,∠CGFの大きさxを求めなさい。 |
ややむずかしい