| 【 後 期 】 次の1~15の中から,指示された8 問について答えなさい。 |
| 1 |
 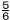 ×(-0.4) ×(-0.4)
|
9 |
距離の測定値6150mの有効数字が上から3桁の6,1,5 のとき,整数部分が1桁の数と10の累乗の積の形で表しなさい。
|
| 2 |
2(3a-2b)-3(2a-b)
|
10 |
 n,Nを自然数とする。N≦√n<N+1を満たすnが31個あるとき,Nの値を求めなさい。 n,Nを自然数とする。N≦√n<N+1を満たすnが31個あるとき,Nの値を求めなさい。
|
| 3 |
比例式 6:8=x:20 のxの値を求めなさい。
|
11 |
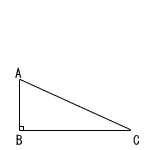 図のように,∠ABC=90°の直角三角形ABCがある。辺CA上に,∠PBA=30°となるような点Pを,定規とコンパスを用いて作図しなさい。ただし,作図に用いた線は消さないこと。 図のように,∠ABC=90°の直角三角形ABCがある。辺CA上に,∠PBA=30°となるような点Pを,定規とコンパスを用いて作図しなさい。ただし,作図に用いた線は消さないこと。 |
| 4 |
|
| 5 |
| 連立方程式 { |
2x+3y=-1 |
| -4x-5y=-1 |
を解きなさい。
|
12 |
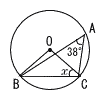 図で,3点A,B,Cは,円Oの周上の点である。このとき,∠xの大きさを求めなさい。 図で,3点A,B,Cは,円Oの周上の点である。このとき,∠xの大きさを求めなさい。
|
| 6 |
方程式 3x2-5x+2=0 を解きなさい。
|
13 |
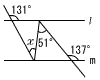 図で,2直線 l,mは平行である。このとき,∠xの大きさを求めなさい。 図で,2直線 l,mは平行である。このとき,∠xの大きさを求めなさい。
|
| 7 |
|
14 |
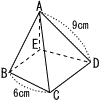  図のような,正四角錐すいA-BCDEがある。底面の1辺の長さが6㎝,側面の二等辺三角形の等しい辺の長さが9㎝である。この正四角錐A-BCDEの体積を求めなさい。 図のような,正四角錐すいA-BCDEがある。底面の1辺の長さが6㎝,側面の二等辺三角形の等しい辺の長さが9㎝である。この正四角錐A-BCDEの体積を求めなさい。
|
| 8 |
a<0のとき,関数 y=ax について必ずいえることを,次のア~エからすべて選んで記号を書きなさい。
| ア |
xが増加すると,yも増加する。 |
| イ |
xが増加すると,yは減少する。 |
| ウ |
xはyに比例する。 |
| エ |
xはyに反比例する。 |
|
|
15 |
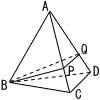  図のような,三角錐(すい)A-BCDがある。点P,点Qは,それぞれ辺AC,辺AD上にある。AP:PC=AQ:QD=3:1であるとする。このとき,三角錐A-BPQの体積は,四角錐B-PCDQの体積の何倍か,求めなさい。 図のような,三角錐(すい)A-BCDがある。点P,点Qは,それぞれ辺AC,辺AD上にある。AP:PC=AQ:QD=3:1であるとする。このとき,三角錐A-BPQの体積は,四角錐B-PCDQの体積の何倍か,求めなさい。
|
 図のように,∠ABC=90°の直角三角形ABCがある。辺CA上に,∠PBA=30°となるような点Pを,定規とコンパスを用いて作図しなさい。ただし,作図に用いた線は消さないこと。
図のように,∠ABC=90°の直角三角形ABCがある。辺CA上に,∠PBA=30°となるような点Pを,定規とコンパスを用いて作図しなさい。ただし,作図に用いた線は消さないこと。 図で,3点A,B,Cは,円Oの周上の点である。このとき,∠xの大きさを求めなさい。
図で,3点A,B,Cは,円Oの周上の点である。このとき,∠xの大きさを求めなさい。 図で,2直線 l,mは平行である。このとき,∠xの大きさを求めなさい。
図で,2直線 l,mは平行である。このとき,∠xの大きさを求めなさい。
