| １ |
 －7－21÷7
|
８ |
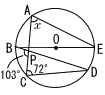 右の図のように,円Ｏの円周上に5つの点Ａ,Ｂ,Ｃ,Ｄ,Ｅがあり,線分BEは円Ｏの直径である。また,線分ACとBDの交点をPとする。∠BPC＝103°,∠PCD＝72°であるとき,∠xの大きさを答えなさい。
|
| ２ |
3(5a－2b)－2(2a－b)
|
| ３ |
－42x2y3÷2xy2×5x2y
|
| ４ |
| 連立方程式 { |
3x＋8y＝9 |
を解きなさい。 |
| x＋4y＝7 |
|
９ |
| 階級(人) |
度数(区数) |
以上 未満
50000～200000 |
3 |
| 200000～350000 |
10 |
| 350000～500000 |
3 |
| 500000～650000 |
2 |
| 650000～800000 |
4 |
| 800000～950000 |
1 |
| 計 |
23 |
次の表は,東京23区のそれぞれの人口を調べ,度数分布表にまとめたものである。このとき,人口の最頻値を答えなさい。
（「日本国勢図会」2016/17年版より作成）
|
| ５ |
√8＋√18－6√2
|
|
| ６ |
2次方程式 x2－8x－7＝0 を解きなさい。
|
|
次の(1)～(4)について,yがxに比例するときは「比例」,yがに反比例するときは「反比例」,yがxに比例も反比例もしないときは「Ｘ」をかきなさい。
(1)
|
縦の長さをxcm,横の長さをycmとする長方形の周の長さが20cmである。 |
(2)
|
100km離れた2地点間を毎時xkmの速さで往復するときにかかった時間がy時間である。 |
| (3) |
半径がxcmの円の面積がycm2である。 |
(4)
|
１個50円の品物をx個買うときの代金がy円である。 |
|
| ７ |
右の図のように,AD//BC,AD:BC＝2:5の台形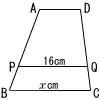 ABCDがある。辺AB上に,AP:PB＝2:1となる点Ｐをとり,点Ｐから辺BCに平行な直線を引き,辺CDとの交点をＱとする。PQ＝16cmのとき,xの値を答えなさい。
|
７ |
ややむずかしい