| １ |
(1)  5－(1－4）
|
５ |
＜選択問題＞
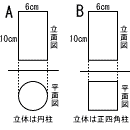
下の図は,数学の授業で学んだ立体を投影図に表したものである。A,Bのどちらか１つを選び,その投影図で表された立体の表面積を求めなさい。なお,円周率はπとし,選んだ投影図の記号を解答欄に書くこと。
|
(2)  － ÷
|
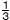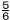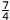
(3) －3a2×(－2b)2÷6ab
|
|
|
| ２ |
x＝－16のとき,x2＋x－20 の値を求めなさい。求め方も書くこと。
|
６ |
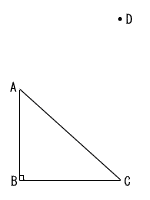
 下の図において,△ABCは,∠ABC＝90°の直角三角形であり,点Dは△ABCの外部の点である。下の【条件】の①,②をともにみたす点Ｐを,定規とコンパスを使って作図しなさい。
ただし,作図に使った線は残しておくこと。
【条件】
①点Ｐは,直線BD上にある。
②∠APB＝∠ACBである。 |
|
| ３ |
2次方程式 (2x－1)(x＋8)＝7x＋4 を解きなさい。解き方も書くこと。
|
| ４ |
下の図は,クラスの生徒33人が夏休みに読んだ本の冊数を,ヒストグラムに表したものである。このヒストグラムにおいて,平均値をa,中央値をb,最頻値をcとするとき,a,b,cの関係を表す不等式として最も適切なものを,あとのア～ウから１つ選び,記号で答えなさい。
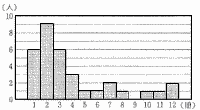
ア a＜b＜c
イ b＜c＜a
ウ c＜b＜a
|
 |
