全国公立高校入試 　１番問題　【平成３０年春】	正　答　１
	１　北海道　〜　８　茨城県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１北海道	１ (1) −27　 　(2) −7＋20＝13 　 (3) 6√2−2√2＝4√2 ２ 2×(−3)2＝2×9＝18 ３ グラフより,傾きa＝2,切片b＝−1 ４ 上式＋下式より,4x＝4で,x＝1 　上式に代入して,1＋y＝7で,y＝6 　よって,x＝1,y＝6 ５ 三平方の定理より, 　√42＋52＝√16＋25＝√41cm ６ S＝4πr2＝4×22π＝16πcm2	４岩手県	１ −4＋7＝3　　２ −5b ３ 3−√3−2＝1−√3 ４ (x＋4)(x−4) ５ 解の公式より， 　x＝ −(−5)±√(−5)2−4×1×3 2×1 　　＝ 5±√13 2 　〜２番問題（おまけ）〜 a＝10x＋7　(a−10x＝7等も可) 　〜３番問題（おまけ）〜 ウ　y＝3x
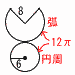２青森県	１ (1) −3　(2)　7−18＝−11 　(3)   9a2b×2×b ＝6ab  3ab 　(4)   (6x＋y)−2(x−7y) ＝ 4x＋15y  4 4 　(5) (x2−2x＋1)−(x2−4x−12)＝2x＋13 ２ a＝5b＋3 ３ 与式＝(√3＋1)(√3−1)＋(√3＋1) 　　＝3−1＋√3＋1＝3＋√3 ４ x2＋4x−5＝0で,(x＋5)(x−1)＝0 　よって,x＝−5,1 ５ 比例定数a＝xy＝(−2)×3＝−6 　y＝ −6 にx＝−4を代入して,y＝− x  ６ 中央値は20人目だから,5〜10冊で10人 　10÷40＝0.25 (も可) ７ (右図参照) 側面の弧＝底面の円周より, ×12π×8＝48πcm2 ８ ∠ACD＝90−42＝48° 　∠BDC＝∠BAC＝32° ∠x＝180−(48＋32)−100°	５山形県	１ (1) 5＋3＝8　(2)  1 −  5×4 ＝ 7−10 ＝−  1  3  6×7 21  7 　(3)   −3a2×4b2 ＝−2ab 6ab 　(4)   　30√6 . −2√6＝ 30√6 −2√6＝3√6 √6√6 6 ２ 与式＝(x＋5)(x−4) 　　＝(−11)×(−20)＝220 ３ 2x2＋15x−8−7x−4＝0 　2x2＋8x−12＝0で,x2＋4x−6＝0 解の公式より, 　x＝−2±√22−1×(−6)＝−2±√10 ４ a＝132÷33＝4,b＝3,c＝2より,ウ ５　選択問題 　Ａ＝10×6π＋32π×2＝78πcm2 　Ｂ＝10×6×4＋62×2＝312cm2 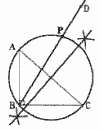６　右図 ACを直径とする円 　・ACの中点を作図 　・中点を中心とする円を作図 円と直線ＢＤの交点Ｐを作図
３秋田県	【前期】 １ −3×(−2)＝6 ２ x＝2×49÷7＝14 ３  2(2x−6)−3(x−1) ＝ 4x−12−3x＋3 ＝ x−9 3×2 6 6 ４ 上式×4＋下式×3より, 　23x＝23で,x＝1 　これを上式に代入して,2＋3y＝−1で,y＝−1 　よって，x＝1,y＝−1 ５ (x＋12)(x−3)＝0より,x＝−12,3 ６ √8−√18＝2√2−3√2＝−√2 ７ 与式＝(504＋496)(504−496) 　＝1000×8＝8000	６宮城県	【前期】 １ −2＋7＝5　　２   4−5 ＝−  1   3  3 ３   4a2b ＝2a　　４ a＞3b＋5  2ab ５ 3xy(x−2y＋6)　　６ 7−2√10 ７ y＝x＋2にx＝2を代入すると,y＝3 　交点(2,3)となり,これをy＝に代入すると,  　3＝  a で,a＝6　よって式は,y＝  6  2  x ８ ＢがＡの約数になる確率は, ･Ａが12の場合は  3 　・Ａが13の場合は  0  3  3 ･Ａが14の場合は  1 　・Ａが15の場合は  1  3  3 ･Ａが16の場合は  2  3 よって,確率＝  1 ×  3 ＋  1 ×  0  5  3  5  3  　＋  1 ×  1 ＋  1 ×  1 ＋  1 ×  2 ＝  7  5  3  5  3  5  3 15 ９ ∠ＡＣＢ＝73−25＝48°＝∠ADB 　円周角が等しく,四角形ABCDは円に内接 　∠BDC＝∠BAC＝55°で， 　∠ACD＝180−(55＋73)＝52°
	【後期】 8問選択 １ (1) 4−15＝−11　　(2) −1×3＝−3 ２  4ab2×（−3a) ＝−2a2b 3×2b ３ 3√3− 　6√3 . 3√3−2√3＝√3 √3√3 ４ 方程式にx＝3を代入して, 　2×3＋a−1＝0より,a＝−5 ５ 与式＝3x−15y−8x＋14y＝−5x−y 　＝−5×−3＝−1−3＝−4 ６ (x−2)(x−3)＝0より,x＝2,3 ７ y＝  a に(3,2）を代入して,2＝  a で,a＝6  x  3 　y＝  6 にx＝−1を代入して,y＝−6  x ８   a ＋ b ＝1  13 18 ９　ア＋イ＝17−(3＋4＋4＋2)＝4 　また,中央値2点は9人目で,アに入る 　よってアは,2〜4人で,3組 10 与式＝√3√102−nより,102−n＝3 　n＝102−3＝99 11 BCは直径だから,∠BDC＝90° 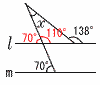　∠ABC＝180−(41＋90) 　　＝49° 12 右図参照 　x＋110＝138より,∠x＝28° 13 右下図参照 　AB//DQとなる平行線を引く 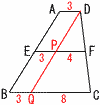　△DPF∽△DQC 　　相似比1:2で,PF＝4 　よって,EF＝3＋4＝7cm 14 円柱A−円柱B (半径4,高さ8の円柱A) 　　＝42π×8＝128π (半径2,高さ4の円柱B) 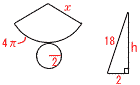　　＝22π×4＝16π よって, 　128π−16π＝112πcm3 15 右上図参照 母線の長さをxとすると, 　表面積＝×4πx＋22π＝40πより,x＝18 高さをhとすると,h2＋22＝182より,h＝8√5cm		【後期】 １ −5　　２ 14 ３ 4x−14y−3x＋9y＝x−5y ４ 与式＝a2＋2b＝32＋2×(−  1 )  2 　＝9−1＝8　　　５ 5−3＝2 ６ (x−5)(x＋4)＝0より,x＝5,−4 ７ あ正,い負,う負だから,あ最大 　い＜う＜0だから,い最小　よって,ア 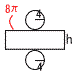８ 比率で考えて,  150 ＝  12 で,x＝1250個  x 100 ９ 球の表面積＝4π×52＝100π 　42π×2＋8πh＝100πより, 　高さh＝ 100π−32π ＝ 17 cm 8π  2
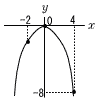		７福島県	１ (1) −5　　(2)  3×5 ＝  3  10×4  8 　(3)   　 6x4 　. ＝−  2 x  −3x2×3x  3 　(4) 4√3−√3＝3√3 ２ 与式＝5x−y＝5×(−)−3＝−4 　〜２番問題（おまけ）〜 １ √28n＝2√7nより,n＝7 ２ 右図参照 　x＝4のとき,y＝42a＝−8で, 　a＝−　　 ３ ウ
		８茨城県	１ −5　　２ 20−18＝2 ３   1 ＋  3×5 ＝ 1＋2 ＝  3  8 10×6 8  8 ４ 8x−12y−3x＋12y＝5x ５ 3√5−√5＝2√5 　〜２番問題（おまけ）〜 １ (x−1)(x−8) ２ 連立方程式 { 5x＋y＝7 …ア  2x−y＝7 …イ  　ア＋イより,7x＝14で,x＝2 　これをアに代入して,5×2＋y＝7で,y＝−3 　　よって,x＝2,y＝−3 ３ 解の公式より， 　x＝−1±√12−1×(−1)＝−1±√2 ４ 8a＋b＜500