全国公立高校入試 　１番問題　【平成２９年春】	正　答　３
	17　石川県　〜　24　三重県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

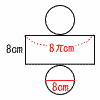17石川県	１ (ア) 5＋3＝8 　 (イ) 4−2＝2 　 (ウ)   3x2y×2 ＝2x  3xy 　 (エ)   4(2a−b)−3(a−b)  3×4 　　＝ 8a−4b−3a＋3b ＝ 5a−b 12  12 　 (オ)   　6√3 . −3√3＝2√3−3√3＝−√3  √3√3 ２ 解の公式より， 　x＝ −(−1)±√(−1)2−4×1×(−3) 2×1 　＝ 1±√13 2 ３（右図参照） 　底面の円周は8πだから， 　側面積＝8×8π＝64πcm2 ４ a−3b≦2 ５ Ａ校 （理由）15分以上20分未満の相対度数 　Ａ校は，20÷80＝0.25 　Ｂ校は，42÷210＝0.2	22静岡県	１ (1) 11−2＝9　　(2)   −9a2×7b ＝3ab  21a 　(3)   5(x＋y)−3(x−2y）  3×5 　　＝ 5x＋5y−3x＋6y ＝ 2x＋11y 15 15  　(4)　6−6√6＋9−3√6＝15−9√6 ２ 与式＝（a＋3b)(a−3b） 　　　＝(37＋36)(37−36)＝73 ３ x2−5x＋2＝0 　解の公式より， 　x＝ −(−5)±√(−5)2−4×1×2 2×1 　＝ 5±√25−8 ＝ 5±√17 2 2 　〜２番問題（おまけ）〜 １ (1.09a＋0.93b)人 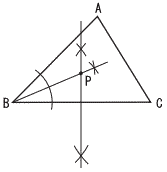２ 右図 ・∠Ｂの二等分線 ・ＢＣの垂直二等分線 ・2線の交点がＰ ３ 合格品の階級 　（54〜56ｇ)の相対 　度数が，Ａ0.95で， 　Ｂ0.94なので， 　Ａが大きい。
18福井県	１ (ア) 2＋18＝20 　（イ) 3√5− 20√5 ＝3√5−4√5＝−√5 √5√5 　(ウ)   8a2b×3ab ＝−2a2b2  −3a ２ (x−1)2＝3 　 x−1＝±√3 　 x＝1±√3 ３ 正しいのは，２と３ 　１は，±2が正しい 　４は，＋8が正しい 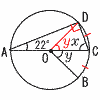４（右図参照） ∠Ｄ＝90°より， 　∠x＝90−22＝68° ∠ＣＯＤ＝∠yより， 　∠y＝22×2＝44° ５ 範囲＝最大値−最小値 ア 最大値＝9のとき，9−Ｈ＝8で，Ｈ＝1 　9＋5＋…＋G＋1＋4＋2=6.0×10 　Ｇ＝60−48＝12（題意に不適） イ 最小値＝2のとき，Ｇ−2＝8で，Ｇ＝10 　9＋5＋…＋10＋Ｈ＋4＋2=6.0×10 　Ｈ＝60−57＝3点（適） 順に並べると，2,3,3,4,5,6,9,9,9,10で， 　中央値＝(5＋6)÷2＝5.5点 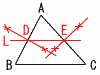６ 右図 　△ＡＤＥ∽△ＡＢＣ 　（相似比1:2)になればよい。 　ＡＢ,ＡＣの中点を結ぶ	23愛知県	【　Ａ　】 １ −4−9＝−13 ２   5(2x−1)−3（3x＋1) ＝ x−8  3×5 15  ３ √6(√3＋√2)(√3−√2） 　＝√6×(3−2)＝√6×1＝√6 ４ x2−8x＋16＋2x−4−3 　＝x2−6x＋9＝(x−3)2 ５ x2−2x−15＝5x−24 　 x2−7x＋9＝0 　解の公式より， 　x＝ −(−7)±√(−7)2−4×1×9 2×1 　＝ 7±√49−36 ＝ 7±√13 2 2 ６ 20x＋16y (点) ７ {  4x−3y＝−7  3x＋2y＝16 　上式×2＋下式×3より， 　　17x＝34で，x＝2 　これを下式に代入して， 　　6＋2y＝16で，y＝5 　よって，x＝2,y＝5 ８ 変化の割合＝  (−3)×32−（−3）×12  3−1 　　＝ −27＋3 ＝−12 2 ９ 1:(4/3)＝3:4で，3/4倍
19山梨県	１ 13−8＝5　　２ 　−12＋15 ＝  1  9  3 ３ 36−16＝20 ４ −√7＋ 14√7 ＝−√7＋2√7＝√7 √7√7 ５ 　16a2b×5b ＝−8a  　−10ab2 ６ 9x＋6y−4x＋8y＝5x＋14y 　〜２番問題（おまけ）〜 １ (x＋4)(x＋6)＝0より，x＝−4,−6 ２ 全部で，4×3＝12通り 　このうち差が2以上は，次の3通り 　　(a，b)＝(9,7) (10,8) (10,7) 　よって，確率＝  3 ＝  1 12  4 ３ ∠Ｂ＝∠Ｃ＝60°だから， 　∠ＢＡＣ＝110−60＝50°		【　Ｂ　】 １ 2−9＝-7 ２   64x2y2×3 ＝48y  4x2y ３ 4√5−3√5＝√5 ４ 与式＝(x＋y)2＝(1.8＋0.2)2＝22＝4 ５ x2−4＝x＋8 　 x2−x−12＝0 　 (x−4)(x＋3)＝0より，x＝4,−3 ６ y−210 (m) ７　(3＋10＋24＋12＋40＋12＋7)÷30 　＝108÷30＝3.6冊 ８　定価x円とすると，0.15x＝240 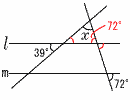　x＝240÷0.15＝1600円 ９（右図参照) 　∠x＝180−39−72 　　＝180−111 　　＝69°
20長野県	１ (1) −3　　(2)   8×(−3) ＝−6  4 　 (3) 2√3＋4√3−√3＝5√3 　(4)   5x＋y−2x＋4y ＝ 3x＋5y  4 4 ２ △ADEで，∠EDB＝20＋37＝57° 　△FDBで，∠x＝97−57＝40° ３ x2＋5x−2＝0 　解の公式より， 　x＝ −5±√52−4×1×(−2) 2×1 　＝ −5±√33 2 ４ それぞれの確率を求めると， ア   3 ×  3 ＝  9  6  6 36 イ  　5 . ＝  5 6×6 36 ウ  　4 . ＝  4 6×6 36 エ  　6 . ＝  6 6×6 36 　よって，ア ５ 移行すると符号が変わるから，ウ 　2a＝b−3m 　a＝ b−3m 2 ６ Ｂの半径をrとすると， 　Ａ＝π(2r)2×4r＝16πr3…ア 　Ｂ＝  4 πr3×  1 ＝  2 πr3…イ  3  2  3 　ア÷イより，16×  3 ＝24杯  2 ７ 弦ＡＢに対する円周角を考え， 　ＢＣを直径とする円を作図する。 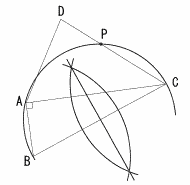・ＢＣの垂直二等 　分線を引く ・ＢＣの中点をとる ・ＢＣを直径とする 　円をかく ・ＣＤとの交点を 　Ｐとする	24三重県	【前期】 １ 7−10＝−3 ２   8x2y×3×(−7xy) ＝7x2  (−4xy2)×6 ３ 与式＝3x−6y−4x＋2y＝−x−6y 　　　＝−2−4×(−3)＝−2＋12＝10 ４ 3√12− 15√3 ＋4√3 √3√3 　　＝6√3−5√3＋4√3＝5√3 ５ 90−3n＞0より，0＜n＜30 　90−3nは平方数だから， 　　90−3n＝1,4,9,25,36, ,81, 　3n＝89,86,81,74,65,54,41,26,9で， 　よって，自然数n＝27,18,3 ６ x2−6x−16＝12−3x 　x2−3x−28＝0 　(x−7)(x＋4)＝0より，x＝7,−4 ７ チョコレート1個x円とすると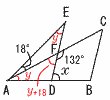， 　24x−100＝20x＋40 　4x＝140より，x＝35(円) よって，35×20＋40＝740円 ８（右図参照） △ＡＢＣ∽△ＥＤＡより， 　∠ＣＡＢ＝∠Ｅ＝yとすると， 　　y＋18＝180−132＝48で，y＝30° 　よって，∠x＝2y＋18＝78° 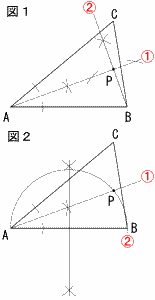９ 解答例は右図 (図1) ・∠Ａの二等分線 ・Ｂから垂線 ・交点がＰ 　または (図2) ・∠Ａの二等分線 ・直径ＡＢの円 ・交点がＰ
21岐阜県	１−12−10＝−22 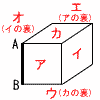２   18ab×8×b ＝48b2  3a ３ x−y＝2√2，xy＝3より， 　与式＝xy(x＋y) 　　＝3×2√2＝6√2 ４（右図参照） 　ウ,カ ５ y＝−2x2≦0だから，エ 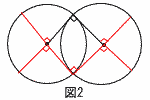６ （右図参照） 　扇形の弧12個分で， (中心角90°半径4cm) 　(8π÷4)×12 　＝24πcm		【後期】 １ 72　　２ 3x−6y−2x＋8y＝x＋2y ３ 2y＝11−3x 　y＝ 11−3x 　または， y＝−  3 x＋ 11 2  2  2 ４ 6−2√6＋√6−2＝4−√6 ５ (x−5)(x＋3) ６ 解の公式より， 　x＝ −(−1)±√(−1)2−4×2×(−2) 2×2 　＝ 1±√1+16 ＝ 1±√17 4 4 ７ (1) 範囲＝最大値−最小値 　　＝90−20＝70点 　(2) 5番目と6番目の平均で， 　　　(50＋60)÷2＝55点