|
�i�U�j�{�錧 | �w�K���@�@�@ ���@�@ �@���i�@�@�@�j |
|
�i�U�j�{�錧 | �w�K���@�@�@ ���@�@ �@���i�@�@�@�j |
| �y�@�O�@�@���@�z | |||||||||||||||||||||||||||||
| 1 | |
�V | �@����N���X�ɂ��āC�}�����̖{�݂̑��o�����������Ƃɒ��ׂ܂����B���̕\�́C���̌��ʂ��܂Ƃ߂����̂ł��B�{�݂̑��o�����̒����l(���W�A��)�����߂Ȃ����B
�@ |
||||||||||||||||||||||||||
| �Q |
�@�@�@ |
||||||||||||||||||||||||||||
| �R | �@(6a�{9b�|3)��(�|3) �@�@�@�@�@�@�@ |
�W | �@���́��Ɏ��������́C���̐}�̔����̃O���t�ɂ��āCy��x�̎��ŕ\�����Ƃ��́Cx��y�̊W�ƁC���萔�Ɋւ��Đ����������̂ł��B�i �@ �j�Ɍ����C( �A )�ɒl�����ꂼ������Ƃ��C���̓��e���������Ȃ�g�ݍ��킹���C���Ƃ̃A�`�J����1�I�сC�L���œ����Ȃ����B
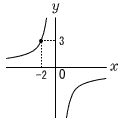 �A�@�@ �a�@�A 1 �A�@�@ �a�@�A 1�C�@�@ �a�@�A 5 �E�@�@ �ρ@�A 6 �G�@�@ �ρ@�A -6 �I�@�@ ���@�A -3/2 �J�@�@ ���@�A -2/3 |
||||||||||||||||||||||||||
| �S |
�@�@�@ |
||||||||||||||||||||||||||||
| �T |
�@ |
||||||||||||||||||||||||||||
| �U | �@2�������� (x�{1)2�|9��0 �������Ȃ����B �@ |
�X | �@���̐}�̂悤�ɁC�����`�a�a�Ƃ��锼�~�n�̌�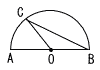 �`�a��ɁC�ʂ`�b�F�ʂb�a��1:2�ƂȂ�_�b���Ƃ�܂��B�`�a��12cm�Ƃ���Ƃ��C��OBC�̖ʐς����߂Ȃ����B �`�a��ɁC�ʂ`�b�F�ʂb�a��1:2�ƂȂ�_�b���Ƃ�܂��B�`�a��12cm�Ƃ���Ƃ��C��OBC�̖ʐς����߂Ȃ����B�@ |
||||||||||||||||||||||||||
| �y�@��@�@���@�z�@ | ||||||||||||||||||||||||||
| 1 | �V | �@����N�̑S���̃R���̎��n�ʂ́C��8439000t�ł����B�L��������8,4,3,9�Ƃ��āC���̎��n�ʂ�(����������1�����̐�)�~(10�̗ݏ�)�̌`�ŕ\���Ȃ����B �@�@ |
||||||||||||||||||||||||
| �Q |
�@�@�@ |
�W | �@���̐}�̂悤�ȁC1�̒�����ɂȂ�3�_�`,�a,�b�ƁC3�̒����`�a,�a�b,�`�b������܂��B���Ƃ́��́C���̐}�ɂ����āC2�_�`,�b���瓙���������ɂ���_�̂����C�������b�`,�b�a�܂ł̋������������_�o���C��}��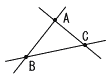 ����ċ��߂���@�ɂ��Đ����������̂ł��B�������������Ȃ�悤�ɁC�i���j�̃A,�C,�E�C(��)�̃G,�I,�J���炻�ꂼ��1�I�сC�L���œ����Ȃ����B ����ċ��߂���@�ɂ��Đ����������̂ł��B�������������Ȃ�悤�ɁC�i���j�̃A,�C,�E�C(��)�̃G,�I,�J���炻�ꂼ��1�I�сC�L���œ����Ȃ����B
|
|||||||||||||||||||||||
| �R | �@a��2,b���|1�̂Ƃ��Ca2�|2b �̒l�����߂Ȃ����B �@�@�@�@�@�@�@ |
|||||||||||||||||||||||||
| �S |
�@�@�@ |
|||||||||||||||||||||||||
| �T | �@x2�|4y2 �������������Ȃ����B �@ |
�X | �@���̐}�̂悤�ɁC�� y��x2�c� �̃O���t��ɁCx���W��2�ł���_�`�ƁC�_�`��y���W��������x���W���قȂ�_�a���Ƃ�C�_�`�Ɠ_�a�����т܂��B�܂��C�� y��1/4x2�c� �̃O���t��ɁCx���W��5�ł���_�b��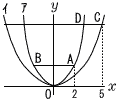 �Ƃ�C�_�b��ʂ�x���ɕ��s�Ȓ����Ɗ� y��x2�̃O���t�Ƃ̌�_�̂����Cx���W�����ł���_���c�Ƃ��܂��B�����`�a�Ɛ����b�c�̒����̔�����߂Ȃ����B �Ƃ�C�_�b��ʂ�x���ɕ��s�Ȓ����Ɗ� y��x2�̃O���t�Ƃ̌�_�̂����Cx���W�����ł���_���c�Ƃ��܂��B�����`�a�Ɛ����b�c�̒����̔�����߂Ȃ����B�@�@�@ |
|||||||||||||||||||||||
| �U | �@��50�|��18�{��8 �@�@�@ |
|||||||||||||||||||||||||
| �m�g�b�v�ɖ߂��n �m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n �m���̃y�|�W�ɐi���n�@ |