全国公立高校入試
　１番問題　【平成２９年春】
正　答　１
１　北海道　〜　８　茨城県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１北海道 １ (1) 6＋7＝13　　(2) 9−32＝−23
　　(3) 15÷3＝5
２ a2−5a−1＋3a2＋6a−12
　　＝4a2＋a−13
３ x＝3，−8
４ ∠x＝62＋41＝103°
５ y＝ax＋bに，(0,1)と(1,4)をすると，
　{  1＝0＋b
 4＝a＋b
　これを解いて，a＝3,b＝1で，y＝3x＋1
　x＝3を代入して，y＝3×3＋1＝10
６ ＰはＱと比較すると，
　・底面積は等しい …ア
　・高さは2倍 …イ
　・形は柱体で，錐体の3倍 …ウ
　ア,イ,ウより，2×3＝6倍　		 ４岩手県 １ −7

２ −3a＋6＋6a−2＝3a＋4

３ 5＋2√5＋1＝6＋2√5

４ x−3x＝−10
　 −2x＝−10より，x＝5

５ (x＋5)(x−7)＝0より，x＝−5,7



　〜２番問題（おまけ）〜

−4＜−3＜＋5　（または，＋5＞−3＞−4）
２青森県 １ (1) −3
　(2)   3 ×(−  1 )＝−  3
 4  4 16
　(3)  4ab2×9a2 ＝18a3
2b2
　 (4) (x2＋10x＋25)−(x2＋2x−13)
　　　 ＝10x−2x＋25＋15＝8x＋40
　 (5) √48＋√3＝4√3＋√3＝5√3
２ 与式＝−2x−4y＋3x＋3y
　　　＝x−y＝3−(−2)＝5
３ 両辺を入れ替えて，  1 ab＝c
 3
　 両辺×  3 より，a＝ 3c
 b b
４ x(x＋4)＝0より，x＝0,−4
５ 24以上は,24,31,32,33,34,41,42,43,44の9個
　よって,確率＝ 　9　. ＝  9
4×4 16
６ 表面積＝4π×52＝100πcm2
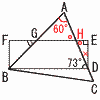７ (右図参照)
　∠H＝90°−∠EDH＝73°
　∠FGB＝180−60−73＝47°
８ 3y＝−2x＋6
　式は，y＝−  2 x＋2
 3
　よってグラフは，
　　切片2，傾き−2/3の直線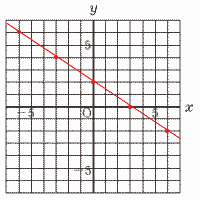
 ５山形県 １ (1) 1−(−2)＝1＋2＝3
　（2)  　8−9 ×  3 ＝−  3 ＝−  1
  12  1 12  4
　（3）   4x2×3y2 ＝2x
 6xy2
　(4) 4＋4√2＋2−3√2＝6＋√2
２　与式＝2(x＋y)(x−y）
　　　＝2×2√5×6＝24√5
３ 4x2＋13x−12＝3x−6
　　4x2＋10x−6＝0
　　2x2＋5x−3＝0
　　（2x−1)(x＋3）＝0より，x＝1/2，−3
４ 取り出し方は全部で，6×6＝36通り
　・差が4は次の4通り
　　　（A,B）＝(1,5) (2,6) (6,2) (5,1)
　・差が5は次の2通り
　　　（A,B）＝(1,6) (6,1)
　差が3以下は，36−(4＋2)＝30通り
　よって，確率＝ 30 ＝  5
36  6
５ （下図参照）
　(A) 垂直 （直交も可）
　(B) 等しい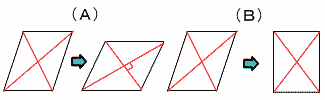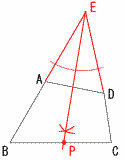




６ 右図
［作図法］
・BAとCDの延長して
　　交点Eをとる
・∠BPCの二等分線l をひく
・l とBCの交点をPとする
３秋田県 　【前期】


１ −11

２ a×(1＋0.08)＝1.08a円　または， 27 a円
25

３ 　1 x−  6 x＝ 5−6 x＝−  x
　2 10 10 10

４ 与式＝ 　3x2y ＝− 3x ＝− 3×2 ＝−2
−xy2 y 3

５ 2つの式に分けると，
　{  x＋y＝5
 2x−3y＝5

　上式×3＋下式より，5x＝20で，x＝4

　これを上式に代入して，4＋y＝5より，y＝1
　　x＝4,y＝1

６ 3√2＋3√3−3√2＝3√3

７ (x＋4)(x−3)＝0より，x＝−4,3

８ 10より大きくなるのは，以下の3通り

　(大,小)＝(5,6) (6,5) (6,6)

　よって，確率＝ 　3　. ＝  1
6×6 12


６宮城県 　【前期】
１ 7−11＝−4　　２ −  1 ＋  3 ＝  1
 4  4  2
３ −2a−3b＋1
４ 7倍して，7c＝a＋b
　　両辺を入れ替えて，a＋b＝7c
　　aを移行して，b＝7c−a
５ 3√5− 10√5  ＝3√5−2√5＝√5
√5√5
６ (x＋1)2＝9より，x＋1＝±3
　x＝±3−1で，x＝2,−4
７ 冊数の順に並び替えると，
　39,88,91,115,130,148,150,161,…,213
　6,7番目の平均で，(148＋150)÷2＝149冊
８ 比例定数a＝xy＝−2×3＝−6で，エ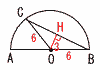
９ ∠BOC＝180×(2/3)＝120°
　OH＝3cm，BH＝3√3cm
　△OBC＝(1/2)×6√3×3
　　　＝9√3cm　
　【後期】
１ −7
２  3×4×(−2) ＝8
−3
３ 22−2×(−1)＝4＋2＝6
４ 上式×2−下式より，x＝7
　これを上式に代入して，
　　2×7＋y＝3で，y＝−11
　x＝7，y＝−11
５ （x＋2y)(x−2y）
６ 5√2−3√2＋2√2＝4√2
７ 8.439×1000000＝8.439×106 ｔ
８ (あ) ウ　　(い) オ
９ A(2,4)，B(-2,4)より，AB＝4
　C(5,25/4)，D(5/2,25/4)より，CD＝5/2
　AB:CD＝4:5/2＝8:5
　【後期】
１ (1) 7−(−2)＝9　　(2) 6−8＝−2
２ 8a−2b−3a＋2b＝5a
３ 与式＝ 3x2×(−2y）2 ＝xy
12xy
　　　＝  1 ×  6 ＝  1 　または0.2
 3 10  5
４ 両辺×12より，
　3(3x−4)＝4(x＋2)で，5x＝20より，x＝4
５ 上式×8−下式より，
　　13y＝−36で，y＝−3
　これを上式に代入して，
　　x−6＝−5で，x＝1
　x＝1,y＝−3
６ 解の公式より，
　x＝ −6±√62−4×2×3 ＝ −6±2√3
2×2 4
　　＝ −3±√3
2
７ 4√2＋3√5−√2−2√5＝3√2＋√5
８ y＝ax＋bに(-3,11)と(2,-4)を代入して，
　{  11＝−3a＋b
 −4＝2a＋b
　これを解いて，b＝2　　よって，アは2
９ ア　最頻値は7人で6冊　×
　 イ　中央値は13番目で5冊　○
　 ウ　範囲は7−1＝6冊　×
　 エ　総合計は14＋42＋20＋12＋4＋1
　　　　　＝93冊　×
　よって，ウ
10 m−2＝1かつn＋3が素数だから，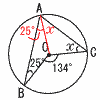
　　m＝3，n＋3＝5,7,11
つまり，m＝3,n＝2,4,8の3組
11 6：ＣＤ＝4:6より，
　ＣＤ＝6×6÷4＝9cm
12 2(∠x＋25)＝134
　∠x＋25＝67より，∠x＝42°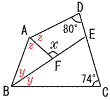
13 右図で∠y,∠zとすると，
　2∠y＋2∠z
　＝360−(80＋74)＝206°
　∠x＝∠y＋∠z＝103°
14 B(−2,2)より，
　　底面が半径2ｃｍの円すいで，
　体積＝  1 ×22π×(6＋2)＝ 32 πｃｍ3
 3 3
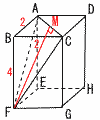15 ACの中点をMとすると，
　△AFMで，
　 AF＝√42＋22＝√20
　 AM＝(√22＋22)÷2＝√2
　FM2＝(√20)2−(√2)2
　FM＝√18＝3√2
　△AFM=2√2×3√2÷2＝6
　表面積＝(2×2÷2)＋6
　　＋(2×4÷2)×2＝2＋6＋8＝16cm2		 ７福島県 １ (1) −42
　(2)  1 −  4 ＝−  3 ＝−  1
 6  6  6  2
　(3） 6a−5b
　(4) √2＋3√2＝4√2

２ ウ


　〜２番問題（おまけ）〜

１ (x＋4)(x−3)＝0より，x＝−4,3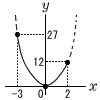

２ （右図参照）
　x＝−3のとき，
　　y＝3×(−3)2＝27
　x＝0のとき，y＝3×02＝0
　x＝2のとき，y＝3×22＝12
　よって，0≦y≦27

３ 7つの三角形に分けれるから，
　三角形7つの総内角−Ｐの回りの角で，
　　ア　180　　イ　360
　
８茨城県 １ −2

２ −12＋18＝6

３  　7×4　. ＋  9 ＝−  4 ＋  9 ＝1
5×(−7)  5  5  5

４ −2x−6y＋x−y＝−x−7y

５  　8√2 . ＋ 3√6 ＝4√2＋3√2＝7√2
√2√2 √3


　〜２番問題（おまけ）〜

１ (x−9)(x＋3)

２ 上式−下式×2より，7y＝−14で，y＝−2
　これを下式に代入して，
　　x−2×(−2)＝6
　　x＋4＝6で，x＝2
　x＝2，y＝−2

３ 解の公式より，
　x＝−4±√16−6＝−4±√10

４ 200−3a＜b

５ 与式＝(x−1)2＝(√5＋1−1)2
　　　＝(√5)2＝5
［トップに戻る］ 　　　　　　　　　　［次ペ−ジに進む］