| 【 後 期 】 次の1〜15の中から，指示された8 問について答えなさい。 |
| 1 |
(1)  7−(−5＋3)
(2) 6＋2×(−4) |
10 |
 m,nは1けたの自然数である。（m−2)(n＋3)の値が素数になるm,nの組は何組あるか,求めなさい。 |
| ２ |
(8a−2b)−(3a−2b) |
11 |
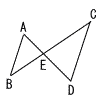 右の図において，AB//CD であり，点Eは線分ADとBCの交点である。AB＝6cm,AE＝4cm,ED＝6cmのとき，線分CDの長さを求めなさい。
|
| ３ |
| x＝ |
1 |
，y＝0.6のとき， |
 |
| 3 |
3x2÷12xy×(−2y）2の値を求めなさい。 |
| ４ |
| 方程式 |
3x−4 |
＝ |
x＋2 |
を解きなさい。 |
 |
 |
| 4 |
3 |
|
12 |
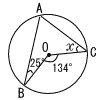 右の図において，3点A,B,Cは，円Oの周上の点である。∠ABO＝25°,∠BOC＝134°のとき，∠xの大きさを求めなさい。
|
| ５ |
| 連立方程式 |
｛ |
x＋2y＝−5 |
を解きなさい。 |
| 8x＋3y＝−1 |
|
13 |
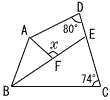 右の図のように，四角形ABCDがあり，点Eは∠ABCの二等分線と辺CDの交点，点Fは∠BADの二等分線と線分BEの交点である。∠ADC＝80°,∠BCD＝74°のとき，∠xの大きさを求めなさい。
|
| ６ |
方程式 2x2＋6x＋3＝0 を解きなさい。
|
| ７ |
√32＋√45−√2(1＋√10)
|
14 |
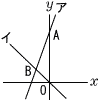 右の図において，アは関数 y＝3x＋8，イは関数 y＝−xのグラフであり，点Aはアとy軸の交点，点Bはアとイの交点である。このとき，直線AOを軸として△OABを1回転させてできる立体の体積を求めなさい。ただし，原点Oから（1,0）,（0,1）までの距離をそれぞれ1cmとする。また，円周率をπとする。
|
| ８ |
次の表は，xとyの関係を表したものである。yが xの1次関数であるとき，表のアにあてはまる値を求めなさい。
| x |
… |
-3 |
… |
0 |
… |
2 |
… |
| y |
… |
11 |
… |
ア |
… |
-4 |
… |
|
| ９ |
| 階級(冊) |
度数(人) |
| 7 |
2 |
| 6 |
7 |
| 5 |
4 |
| 4 |
5 |
| 3 |
4 |
| 2 |
2 |
| 1 |
1 |
| 合計 |
25 |
ある学級の生徒全員について，読書週間に読んだ本の冊数を調べた。右の度数分布表は，その結果をまとめたものである。この表から必ずいえることを，次のア〜エの中から1つ選んで記号を書きなさい。
ア 最頻値は7冊である
イ 中央値は5冊である
ウ 分布の範囲は7冊である
エ 全員の読んだ本の冊数の合計は110冊である |
15 |
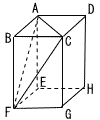 右の図のように，AB＝BC＝2cm,BF＝4cmの直方体ABCD-EFGHがある。この直方体を頂点A,C,F を通る平面で分けたときにできる三角錐すいB-AFCの表面積を求めなさい。
|
