全国公立高校入試 　１番問題　【平成２８年春】

（24）三重県

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

【　前　期　】		【　後　期　】
１	8−5×(−22)	１	2＋5×(−3)
２	5x＋4y − 3x−4y  3 2	２	1 (6a＋4)  　　2
３	x＝3，y＝−4のとき，3x2y＋2xy×(−6y)の値を求めなさい。	３	10x2y÷(−12xy)
４	√32− 4 ＋√50 √2	４	(√3＋√5)(3√3−√5)
５	二次方程式 (x＋1)(x−3)＝12 を解きなさい。	５	9x2−49 を因数分解しなさい。
６	ある数xに4を加えた数の5倍は，xを2倍して4をひいた数に等しくなる。ある数xを求めなさい。	６	二次方程式 2x2−3x-1＝0 を解きなさい。
７	100 円，50円，10円の硬貨が1枚ずつある。これら3枚の硬貨を同時に投げるとき，表が出た硬貨の合計金額が，60円以上になる確率を求めなさい。	７	階級(kg) 度数(人) 　以上　未満 10〜　15   ２ 15〜　20  ３ 20〜　25 ７ 25〜　30 10 30〜　35 ８ 35〜　40 ４ 35〜　45 １ 計 35 　右の表は，ある中学校の2年生35人の握力を調べて度数分布表に整理したものである。この表から，2年生35人の握力の最頻値を求めなさい。
８	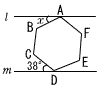右の図のように，正六角形ＡＢＣＤＥＦの頂点Ａを通る直線をl，頂点Ｄを通る直線をmとする。l //mのとき，∠xの大きさを求めなさい。
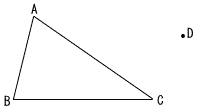
９	右の図で，△ＡＢＣの∠Ｂの二等分線上に，ＣＰ＋ＤＰを最短にする点Ｐを，定規とコンパスを用いて作図しなさい。 　なお，作図に用いた線は消さずに残しておきなさい。