全国公立高校入試 　１番問題　【平成２８年春】

（３）秋田県

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

【　前　　　期　】
１	10−6÷(−2)	〜　２番問題　（おまけ）　〜
２	１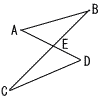枚xgの便せん３枚を，ygの封筒に入れたとき，全体の重さは25ｇよりも軽かった。この数量の関係を不等式で表しなさい。	１	次の図で，線分ＡＢと線分ＣＤは，ＡＢ＝ＣＤ，ＡＢ//ＣＤである。線分ＡＤと線分ＢＣの交点をＥとするとき，△ＡＥＢ≡△ＤＥＣとなることを証明した。ア，イにあてはまる適切な式や言葉を書きなさい。 ［証明］　△ＡＥＢと△ＤＥＣにおいて 　仮定から， ＡＢ＝ＤＣ　　　　･･･　(1) 　平行線の錯角は等しいから， 　　　∠ＡＢＥ＝∠ＤＣＥ　　　　･･･　(2) 　 （ア　　　　　　　　　　　） ･･･　(3) (1)(2)(3)より， 　（イ　　　　　　　　　　　　　　）が 　　　それぞれ等しいから，△ＡＥＢ≡△ＤＥＣ
３	2x＋3 − x＋2  を計算しなさい。  　　5　 　3　 計算の過程も書きなさい。 （過程）
４	連立方程式 ｛  4x＋7y＝2 を解きなさい。  2x＋y＝6	２	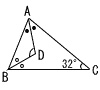次の図の△ＡＢＣにおいて，∠ＡＣＢ＝32°である。∠Ａの二等分線と∠Ｂの二等分線の交点をＤとするとき，∠ＡＤＢの大きさを求めなさい。
５	√72−3√2＋√8	３	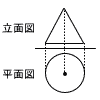次の図は，円錐の投影図であり，立面図は１辺の長さが6cmの正三角形である。このとき，この円錐の体積を求めなさい。ただし，円周率はπとする。
６	方程式　(x＋2)2−49＝0　を解きなさい。
７	yはxに反比例し，x＝4のときy＝6である。x＝−3のときのyの値を求めなさい。	４	2つの関数y＝ax2とy＝−3x＋8 において，xの値が1から3まで増加するときの変化の割合が等しくなる。このとき，aの値を求めなさい。
８	Ａ，Ｂ，Ｃの3人でじゃんけんを1回だけする。このとき，Ａだけが勝つ確率を求めなさい。	５	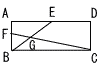次の図で，四角形ＡＢＣＤは長方形である。点Ｅは辺ＡＤの中点，点Ｆは辺ＡＢ上の点で，ＡＦ:ＦＢ＝2:3である。線分ＢＥと線分ＣＦの交点をＧとするとき，ＣＧ:ＧＦを求めなさい。

印刷時に改ページ

【　後　　　期　】
１	(1)　　5−3×(−2) (2)　　−20÷5−(3−5)	９	ある生徒の3教科のテストのそれぞれの点数が70点，80点，a点で，その平均点はb点であった。このとき，aをbを用いた式で表しなさい。
２	(−2x)2÷3xy×(−6x2y)	10	√72n 　が自然数となるような整数nの 7 うち，最も小さい値を求めなさい。
３	x＝7，y＝5のとき，x2y−xy2 の値を求めなさい。	11	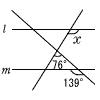右の図で，2直線 l，mは平行である。このとき，∠xの大きさを求めなさい。
４	方程式  　4 x＋3＝  1 を解きなさい。 　5  2 計算の過程も書きなさい。	12	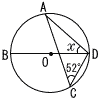右の図で，4点 A，B，C，D は，円Oの周上の点であり，線分BDは円Oの直径である。∠ACD ＝52°のとき，∠xの大きさを求めなさい。
５	連立方程式 ｛  y＝3x＋8 を解きなさい。  4x＋3y＝11	13	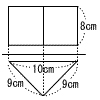右の図は，三角柱の投影図である。この三角柱の体積を求めなさい。
６	方程式　(x−7)(x＋4)＝4x−10 を解きなさい。  計算の過程も書きなさい。	14	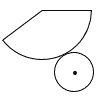右の図は，円錐すいの展開図であり，側面となるおうぎ形は，中心角が135°で面積が24πcm2である。この円錐の底面となる円の半径の長さを求めなさい。ただし，円周率をπとする。
７	√45− 　5 . √5	15	右の図で，三角形ABCは AB＝AC＝6cm，BC＝4cmの二等辺三角形であり，点Dは辺AC上の点である。線分 BDの長さが最も短くなるとき，線分BDの長さを求めなさい。
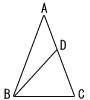８	xはyの2乗に比例し，x＝3のとき，y＝−36である。このとき，yをxの式で表しなさい。