全国公立高校入試
　１番問題　【平成２８年春】
正　答　１
１　北海道　〜　８　茨城県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１北海道 １　(1)　−1

　　(2)　16×5＝80

　　(3)　7√6−√6＝6√6

２　傾きa＝2で，切片b＝3だから，

　　　　y＝2x＋3

３　∠x＝40×2＝80°

４　奇数は4個だから，確率＝  4
 7

５  　x　. ＝ 　2 . より， 
9000 300

　　x＝9000×2÷300＝60個

６　ＢＤ＝√22＋32＝√13cm


　		 ４岩手県 １　−2
２　6a＋3−4a−2＝2a＋1
３　2√3−√3＝√3
４　(x＋5)(x−3)
５　上式−下式×3より，
　　　　2x＝−2で，x＝−1
　　これを下式に代入して，
　　　　−1＋y＝2で，y＝3
　　よって，x＝−1，y＝3

　〜　２番問題（おまけ）　〜

　　0.03a 人　　または   3 . a 人 
100

　〜　３番問題（おまけ）　〜

１　y＝3xにx＝6を代入して，
　　　y＝3×6＝18
２　グラフより，
　　　x＝2のとき，y＝3
　　　x＝6のとき，y＝1
　この区間で連続しているから，
　　　1≦y≦3
２青森県 １　(1)　3＋2＝5
　　(2)　9−5＝4
　　(3)　2x2−5x−3x2＋2x＝−x2−3x
　　(4) −4a2×18b ＝−8a 
9ab
　　(5)　3＋2√3＋1＝4＋2√3

２　−3x−5＜7
３　2つの式に分けると，
　　｛ 3x＋4y＝2
x＋y＝2
　　上式−下式×3より，y＝−4
　　これを下式に代入して，
　　　　x−4＝2で，x＝6
　　よって，x＝6，y＝−4
４　x−2＝±9より，x＝±9＋2
　　　　よって，x＝11，−7
５　y＝axに(−3，2)を代入すると，
　　　2＝−3aより，a＝−  2
 3
　y＝−  2 xにy＝5を代入すると， 
 3
　　5＝−  2 xで，x＝5×(−  3 )＝− 15
 3  2  2
６　取り出し方は全部で4×3÷2＝6通り
 出  1･2  1･3  1･4  2･3  2･4  3･4
 残  3･4  2･4  2･3  1･4  1･3  1･2
　　条件に合うのは，表の赤字で2通り
　　よって，   2 ＝  1
 6  3
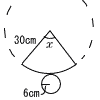７　（右図参照）
　おうぎ形の弧＝円周だから，
　　60π×  x . ＝12π
360
　　x＝12π÷60π×360＝72°
８　等底で等高な三角形を探す
　　△ＡＣＦ，△ＡＤＥ，△ＣＤＦ		 ５山形県 １　(1)　−5＋9−1＝3
　　(2) −8×3 ＋  5 ＝ −8＋5 ＝−  3 ＝−  1
 9×2  6 6  6  2
　　(3) −8ab ＋ 12b2 ＝−4a＋6b
2b 2b
　　(4)　4−4√3＋3＋2√3＝7−2√3
２　与式＝(x−5y)2＝(  5 −5×  3 )2 
 2  2
　　　＝( 5-15  )2＝(−5)2＝25 
2
３　3x2−x−14−5x＋11＝0
　　3x2−6x−3＝0
　　　x2−2x−1＝0
　　解の公式より，
　　　x＝−(−1)±√(−1)2−1×(−1)
　　　　＝1±√1＋1＝1±√2
４　2枚同時に取り出す方法は全部で，
　　　　6×5÷2＝15通り
　　このうち，積が4の倍数になるのは，
　　(2,4) (2,6) (3,4) (4,5) (4,6) (4,7)の6通り
　よって，1−  6 ＝  9 ＝  3
15 15  5
５　＜選択問題＞
（Ａ）　全部の小豆をx粒とすると，
 　10 ＝ 200 より，x＝200×160÷10＝3200
　160  x
　　　よって，およそ3200粒
（Ｂ）　全部のクリップをx個とすると，
 120 ＝ 　x　. より，x＝1000×120÷50＝2400
　50 1000
　　よって，およそ2400個
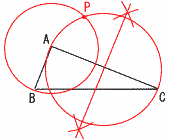６　（右図）

(1)　円Ａ（半径ＡＢ）
(2)　直径ＡＣの円
(3)　2円の交点がＰ
３秋田県 　　【前期】


１　10＋3＝13
２　3x＋y＜25
３ 3(2x＋3)−5(x＋2) ＝ 6x＋9−5x−10
5×3 15
　＝ x−1
15
４　上式−下式×2より，
　　　　5y＝−10で，y＝−2
　　これを下式に代入して，
　　　　2x−2＝6で，x＝4
　　よって，x＝4，y＝−2
５　6√2−3√2＋2√2＝5√2
６　(x＋2)2＝49より，x＋2＝±7
　　x＝±7−2で，x＝5，−9
７　y＝  a に(4，6)を代入すると， 
 x
　　6＝  a で，a＝6×4＝24
 4
　y＝ 24 にx＝−3を代入して，y＝−8
 x
８　手の出し方は全部で，33＝27通り
　　このうちＡだけが勝つのは，次の3通り
　　(A，B，C)＝(ｸﾞ，ﾁ，ﾁ)　(ﾁ，ﾊﾟ，ﾊﾟ)
　　　　　　　(ﾊﾟ，ｸﾞ，ｸﾞ)
　よって，  3 ＝  1
27  9


　〜　２番問題（おまけ）　〜

１　ア　∠BAE＝∠CDE
　　イ　１組の辺とその両端の角
２　∠A＋∠B＝180−32＝148°
　　よって，∠ADB＝180−148÷2＝106°
３　立面図より，高さ＝√62−32＝√27＝3√3
　　体積＝(1/3)×32π×3√3＝9√3πcm3
４　変化の割合＝ 32a−12a ＝−3
3−1
　　4a＝−3で，a＝−  3
 4
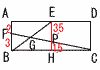５　（右図参照）
　Hは中点で，FB:PH＝3:1.5
　FB:PE＝3:3.5より，
　　　FG:PG＝3:3.5
　よって，CG:GF＝(3＋3.5＋3.5):3
　　　　　　　　　　＝10:3		 ６宮城県 　【前期】
１　5　　　２　−  7 ＋  2 ＝−  5
 3  3  3
３  3a2×2a ＝  3 a
 4a  2
４　上式＋下式×2より，
　　　　7y＝21で，y＝3
　　これを上式に代入して，
　　　　2x＋3＝5で，x＝1
　　よって，x＝1，y＝3
５　3√2−√3−√2＝2√2−√3
６　それぞれにx＝2を代入すると，
　ア　(−2)2≠0　　　イ　4×0＝0
　ウ　4＝−2＋6　　　　エ　4−2≠0
　　　よって，イ，ウ
７　立方体は，1辺をaとすると，体積＝a3
　　正四角錐は，高さが(2/3)aで，
　　　 体積＝  1 a2×  2 a＝  2 a3
 3  3  9
　　よって，2/9倍
８　順番は全部で，4×3×2×1＝24通り
　　このうち，1番目はＡかＤの2通りだから，
　　　確率＝  2 ＝  1
24 12
９　l が(a，0)を通るとすると，
　Ａ(a，a2)，Ｂ(a，a2/3)，Ｃ(a，−a2/2)
　ＡＢ:ＢＣ＝(a2−  a2 ):(  a2 ＋  a2 ) 
 3  3  2
　　　＝  2 a2:  5 a2＝4:5
 3  6
　【後期】
１　7＋2＝9　　　２　−5＋18＝13
３　3x−y−2x−6y＝x−7y
４　2b＋c＝3aで，c＝3a−2b
５　4√3−  9√3 ＝4√3−3√3＝√3
√3√3
６　(x＋8)(x−2)＝0より，x＝−8，2
７　y＝  a に，(2,3)を代入すると，a＝6 
 x
　y＝ 6 にx＝-4を代入して，y＝  6 ＝−  3
x  -4  2
８  　300　. ＝  16 より，x＝6000粒
x＋300 336
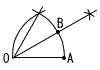９　（右図）
・ＯＡを1辺とする正三角形を
　　かく
・∠Ｏの二等分線をひく
・弧との交点をＢとする 
　　【後期】

１　(1)　5＋6＝11
　　(2)　−4＋2＝−2
２ 4x2×(−6x2y) ＝−8x3
3xy
３　与式＝xy(x−y)＝7･5(7−5)＝35×2＝70
４　両辺×10より，8x＋30＝5x
　　3x＝−30で，x＝−10

５　上式を下式に代入すると，
　　　　4x＋3(3x＋8)＝11
　　　　13x＋24＝11で，x＝−1
　　これを上式に代入して，
　　　　y＝−3＋8＝5
　よって，x＝−1，y＝5

６　x2−3x−28＝4x−10
　　x2−7x−18＝0
　　(x−9)(x＋2)＝0より，x＝9，−2
７　3√5− √5√5 ＝3√5−√5＝2√5 
√5
８　y＝ax2に(3,−36)を代入すると，
　　−36＝9aで，a＝−4（比例定数）
　　よって，y＝−4x2

９　70＋80＋a＝3bより，a＝3b−150
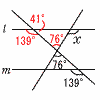10　与式＝  6 √2nだから，n＝2×72＝98
 7
11　（右図参照）
　∠x＝41＋76＝117°

12　∠Ｂ＝∠Ｃ＝52°
　　∠ＢＡＤ＝90°だから，
　　∠x＝180−52−90＝38°

13　√92−52＝√56＝2√14
　体積＝(  1 ×10×2√14)×8＝80√14cm3
 2
14　おうぎ形の半径をrとすると，
　　πr2× 135 ＝24πより，r＝8
360
　　おうぎ形の弧＝底面の円周だから，
　　　16π× 135 ＝2πxで，x＝3cm
360
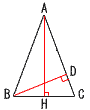15　（右図参照）
　最短は，BD⊥ACのとき
　AH＝√62−22＝4√2cm
　△BDC∽△AHCより，
　　4:6＝BD:4√2で，
　BD＝ 4×4√2 ＝  8 √2cm
6  3
７福島県
１　(1)　−9　　　(2)  4×1 ＝−  1
3×(−8)  6
　　(3) 9x3×x2 ＝3x4
3x
　　(4)　3√3＋  　3√3 ＝3√3＋√3＝4√3
√3√3
　【別解】 3√3＋ √3√3 ＝3√3＋√3＝4√3 
√3
２　y＝axに，(2，−6)を代入すると，
　　−6＝2aで，a＝−3
　よって，y＝−3x

　〜　２番問題（おまけ）　〜

１　(1−0.3)a×10＝7a 円
２　下式を上式に代入して，
　　　　3(1−y)＋4y＝5
　　　　−3y＋4y＝5−3で，y＝2
　　これを下式に代入すると，
　　　　x＝1−2＝−1
　　よって，x＝−1，y＝2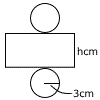
３　（右図参照）
　底面の円周は6πcmで，
　　これは側面の横と等しい
　高さをｈcmとすると，
　　6πｈ＝54πで，
　　　　ｈ＝9cm
 ８茨城県 １　−9
２　15＋1＝16
３  　5 −  4×3 ＝  5 −  1 ＝  3 ＝  1
　6  9×4  6  3  6  2
４　6x＋3y−5x−5y＝x−2y
５　√12＋ 3√3. ＝2√3＋√3＝3√3
√3√3

　〜　２番問題（おまけ）　〜

１　(x＋4)2
２　上式＋下式×4より，
　　　　11x＝−11で，x＝−1
　　これを上式に代入して，
　　　　−3＋4y＝1で，y＝1
　　よって，x＝−1，y＝1
３　解の公式より，
　x＝ −7±√72−4×1×1
2×1　
　　＝ −7±√49−4 ＝ −7±3√5
2 2
４　300a＋7b≦2500
５　与式＝x(x−y)＝(3＋√3)(3−√3)
　　　　　＝9−3＝6

［トップに戻る］ 　　　　　　　　　　［次ペ−ジに進む］