全国公立高校入試 　１番問題　【平成２７年春】		正　答　３
		17　石川県　〜　24　三重県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

17石川県	１ (1)　5＋6＝11　　(2) 4−18÷9＝4−2＝2 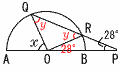　(3)   10a3b2 ×  　　9　 ＝6a   3  5a2b2 　(4)   5(3x−y)−2(7x＋y)  2×5　　 　　　　＝  15x−5y−14x-2y ＝  x−7y  10  10　 　(5)   12×√6 ＋2√6＝2√6＋2√6＝4√6  √6×√6 ２ 解の公式より， 　x＝  −(−1)±√(−1)2−4×3×(−1)  2×3　 　　＝  1±√1＋12 ＝   1±√13  6　  6 ３（右図参照） 　∠y＝28＋28＝56° 　∠ＱＯＲ＝180−2∠y 　　＝68° 　∠x＝180−(68＋28) 　　　＝180−96＝84° ４　ひき方は全部で6通り 　　このうち，和が3の倍数となるのは， 　　　(1，2)　(2，4)　の2通り 　よって求める確率は，   2 ＝  1  6  3 ５ 10冊以上は28人で， 　　28÷40＝0.7（7割）で， 　　　8割以上でない	21岐阜県	１　2−12＝−10　　　２   15xy×8 ＝24x   5y ３   　1×√5 ＝ √5 ＝ 2.236 ＝0.4472≒0.45  　√5√5  5  　5　 ４　∠A＝∠C＝110°より， 　　∠x＝180−(28＋110)＝180−138＝42° ５　立体＝円すい＋円柱 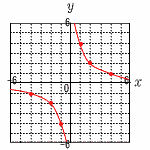 　＝  1 π×32×3＋π×32×3  3 ＝9π＋27π＝36πcm3  ６　（答は右図） 〜２番問題（おまけ）〜 １　x＝−6のとき， 　　y＝1/2×(−6)2＝18 　　　よって，0≦y≦18 ２　A(−6，18)　B(4，8)より， 　傾き＝   8−18 . ＝ −10 ＝−1 4−(−6)  10 　(4，8)を通るから，y＝−(x−4)＋8で， 　　y＝−x＋12 ３　y＝−x＋12にy＝0を代入して， 　0＝−x＋12 　x＝12より，C(12，0)  　ABのx座標の差 ＝ 4−(−6) ＝ 10 ＝  5 倍  　BCのx座標の差 　12−4   8  4
18福井県	１　(1)　3−10ー−7　　　(2)  8xy2 ＝−4xy   −2y 　　(3)　3√2＋  3√2 ＝3√2＋  3 √2＝  9 √2  √2√2  2  2 2　x−2＝Ａとすると， 　与式＝Ａ2＋4Ａ−12＝(Ａ＋6)(Ａ−2) 　　＝(x−2＋6)(x−2−2)＝(x＋4)(x−4) ３　(150×3＋170×6＋190)÷10 　＝(450＋1020＋1+90)÷10＝166点 ４　y＝ax2に(1，3)を代入して， 　　　　3＝a×12より，a＝3 　　y＝3x2にx＝2を代入して，y＝3×22＝12 ５　体積＝半球−円すい 　　　＝  4 π×33×  1 −  1 π×32×3  3  2  3 　　　＝18π−9π＝9πcm3 ６　△DPQ＝xとすると， 　△OPQ∽△DEC（相似比1:2）より， 　　　△DEC＝4x 　△DBE＝△DECより，△DBC＝4x×2＝8x 　△ADC＝△DBEより，△ABC＝8x×2＝16x 　　　よって，16倍	22静岡県	１　(1)　15＋3＝18　　(2)   16a2×b ＝2a   8ab 　(3)   7(x＋y)−2(x−6y) ＝  7x＋7y−2x＋12y  2×7　　  14 　　＝  5x＋19y  14 　(4)　3−5√3＋4√3＝3−√3 ２　与式＝(a−3b)2＝(5−3×  7 )2   3 　　　＝(5−7)2＝(−2)2＝4 ３　移項して，x2−5x＋3＝0 　解の公式より， 　x＝  −(−5)±√25−4×1×3) ＝  5±√13  2×1  2 　〜　２番問題（おまけ）　〜 １   19a＋b  20
19山梨県	１　4＋8＝12 ２　4.5 ３　4＋6＝10 ４　√2−2√2＝−√2 ５　−3a2b ６　−10＋5x−3x−7＝2x−17 　〜　２番問題（おまけ）　〜 １　(x−8)(x＋2)＝0より，x＝8，−2 ２　778300000＝7．783×100000000 　　＝7.783×108 km ３　xy＝12より，積が12で，イ 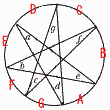４　（右図参照） 　∠aは弧Ａに対する円周角 　∠bは弧Ｂに対する円周角 　　　　　・・・・・・・・・・・ 　∠gは弧Ｇに対する円周角 　弧Ａ＋弧Ｂ＋･･･＋弧Ｇは円周 　弧の和＝中心角の和÷2より， 　　∠a＋∠b＋･･･＋∠g＝360÷2＝180° 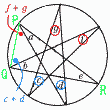【別解】　（右図参照） 　△PQRを考えると， 　∠a＋∠b＋･･･＋∠gは 　△PQRの内角の和で， 　∠a＋∠b＋･･･＋∠g 　　＝180°	23愛知県	【　A　】 １　13−8＝5　　　２   　9×8 ＝  2  　4×27  3 ３　x2＋x−20＝(x＋5)(x−4) ４　7x＋y＝25　（y＝25−7x　等も可） ５　√3(3√3−2√3)＝√3×√3＝3 ６　移項して，x2−x−3＝0 　解の公式より， 　x＝ −(−1)±√1−4×1×(−3) ＝ 1±√13 2×1 2 ７　52：22＝400：Gより， 　G＝4×400÷25＝64cm2 　【　B　】 １　2＋15＝17 ２  4(2x−3y)−6(x−2y) ＝ 8x−12y−6x＋12y  6×4　 24 　＝   2x ＝   x 　 （  1 xも可）   24 12 12 ３ (2√3＋√5)(2√3−√5)＝(2√3)2−(√5)2 　　＝12−5＝7 ４   10a2b×2ab ＝5a   4a2b2　 ５　x2−9−x2＋6x−9−6x＝−18 ６　両辺を2で割ってx2＋2x−3＝0 　　(x＋3)(x−1)＝0より，x＝−3，1 ７　5x＜2y−7
20長野県	１ (1)　−7　　　(2) 36÷(−9)＝−4 　(3) √3(3√2−√2)＝√3×2√2＝2√6 　(4)  6x＋3y＋x−2y ＝ 7x＋y  3 3 ２ (2n＋1)＋2＝2n＋3 ３ 上式を下式に代入して， 　2x−3(x−4)＝5 　2x−3x＝5−12より，x＝7 ４　解の公式より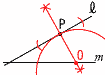， 　x＝ −1±√1−4×2×(−2) ＝ −１±√17 2×2 4 ５ 各辺を2乗して，5＜a＜8だから，a＝6，7 ６（答は右図） 　�@ Pからl の垂直二等 　　　　　分線を引く 　�A mとの交点をOとする ７　ＦＤ:12＝4:(4＋6)より， 　ＦＤ＝12×4÷10＝ 48 ＝ 24 cm（4.8cmも可） 10  5	24三重県	１　−36 ２   10−9 ＝  1   3×5 15 ３　−7a−14b＋6a−2b＝−a−16b ４　(2√7)2−(√5)2＝4×7−5＝23 ５　(x−6)(x＋1) ６　解の公式より， 　x＝ −1±√1−4×2×(−5) ＝ −1±√41 2×2 4 ７　追加分の酢をxmLとすると， 　8:5＝200:(80＋x) 　　8(80＋x)＝5×200で，8x＝1000−640 　　8x＝360より，x＝45mL