全国公立高校入試 　１番問題　【平成２６年春】		正　答　３
		17　石川県　〜　24　三重県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

17石川県	１　(1)　−11　　(2)　16＋4＝20 　 (3)   　15x3y3 ×  　4　. ＝10x2y   　　　2  3xy2 　 (4)  　3(3a＋b)−4(a−b)  ＝  　5a＋7b  　　　　　　　12 　　　12　    (5)　√12＋  9×√3 . ＝2√3＋3√3＝5√3  √3×√3 ２　(x＋1)2＝4より，x＋1＝±2 　　　よって，x＝±2−1だから，　x＝1，−3 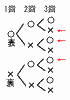３　右の樹形図を参照 　　　　出方は8通りで，3/8 ４　∠x＋15＝110÷2＝55 　　　　よって，∠x＝40° ５　20番目以内 　（理由）　中央値は3冊だから， 　　　花子さんの4冊はそれより多い。	21岐阜県	１　−4−3＝−7 ２　4a−6b−a＋5b＝3a−b ３　与式＝(x＋2)2＝(√5−2＋2)2＝(√5)2＝5 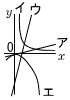４　（右図参照）　イ，エ ５　3.0×105 km ６　△BCDは二等辺三角形だから， 　　　∠BDC＝(180−30)÷2＝75° 　　ACは直径だから，∠ADC=90° 　　　∠ADB＝90−75＝15° 　　よって，　x＝180−(15＋30)＝135 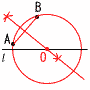７　右図 　(1)　線分ABの⊥二等分線を引く 　(2)　l との交点が中心O 　(3)　OAを半径とする円をかく。
18福井県	１　(1)　9−6＋4＝7 　　(2)   　2(3x−2)−(x−3)  ＝ 6x−4−x＋3   　　　　　　4　　　　  　　　　4　　　 　　　　＝  5x−1   　 4 　　(3)　−√28÷√14＝−√2 ２　x2−x＝12−2xより，x2＋x−12＝0 　　　（x＋4)(x−3)＝0で，x＝−4，3 ３　上式−下式×2より，7y＝14で，y＝2 　　これを下式に代入して，2x−10＝4で，x＝7 　　　よって，x＝7，y＝2 ４　与式＝3√10×√nだから，n＝10 ５　∠ＡＤＢ＝∠ＡＣＤ＝45° 　　△ＡＢＤで，∠x＝180−46−(46＋18)＝70° ６　中点連結定理より，ＰＱＲＳは平行四辺形 　　平行四辺形が正方形となるには， 　　　　対角線が等しく，直交すればよい。 　　よって，ＡＣ＝ＢＤ　と　ＡＣ⊥ＢＤ	22静岡県	１　(1)　9−12＝−3 　　(2)　3a−2b 　　(3) 　9x−3y−4x−4y ＝ 5x−7y  　　　　　12　   　12   (4)　3√3＋ 　15×√3 ＝3√3＋3√3＝8√3 √3×√3 ２　与式＝4a2＋12a＋9−4a2−20a＝−8a  　　　　＝−8×(  1 )＋9＝1＋9＝10  8 ３　x＝3を代入すると，32−3a＋2a＝0 　　9−a＝0より，a＝9 　　x2−9x＋18＝0 　　(x−3)(x−6)＝0より，x＝6
19山梨県	１　−4 ２  　3＋2 ×(−18)＝− 5×18 ＝−10   　　9　  　9　 ３　−4＋16＝12 ４　3√5−  10×√5 ＝3√5−2√5＝√5 √5×√5 ５ 　16ab2 ＝−2b  　−8ab  ６　12x−3y−10x＋4y＝2x＋y 　【２番問題おまけ】 １　解の公式より， 　　　x＝  −7±√72−4×2×1 ＝  −7±√41  　　　　　　2×2　　　　  　　　4　　　 ２　範囲＝最大値−最小値＝70−28＝42点 ３　3：50＝x：1000より，x＝ 3×1000 ＝60   　　50 　　よって，およそ60個	23愛知県	【Ａグループ】 １　−3＋9＝6　　　２　(16/7)×(−7/4)＝−4 ３　上式−下式×2より，9y＝−9で，y＝−1 　　これを下式に代入して，x＝3，y＝−1 ４　与式＝x2−6x−16＋16−x2＝−6x 　　　　　＝−6×250＝−1500 ５　4√5−3√5＝√5 ６　x2−8x＋7＝0 　　(x−1)(x−7)＝0より，x＝1，7 ７　（省略） 【Ｂグループ】 １　−6＋20＝14 ２   　7a ＋ 3ab2×4 ＝ 7a＋3a ＝2a  　 5 　4×5b2 　　5　  ３　3＋2√6＋2−2√6＝5 ４　2(x−3)＝8×3 　　　　2x＝30より，　x＝15 ５　(x−8) ｛ 2(x−5)−(x−8) ｝ 　　＝(x−8)(2x−10−x＋8)＝(x−8)(x−2) ６　2x2−3x−1＝0 　　　解の公式より， 　　x＝ 3±√9＋8 ＝ 3±√17   　　2×2　　 　　4　 ７  　(1/3)×62−(1/3)×32 ＝  12−3 ＝3 　　　　　　6−3　　　   　　3
20長野県	１　(1)　−3 　　(2)　−48 　　(3)　−4＋6×(3/2)＝−4＋9＝5 　　(4)  　5(x−y)−2(2x−y)  ＝ 5x−5y−4x＋2y  　　　　　　2×5　　　  　　　　10　　　　 　　　＝   x−3y  　10 　　(5)　4√2＋2√2−√2＝5√2 ２　1，-2，-3，-4 のいずれか ３　x2−x−1＝0 　　解の公式より， 　x＝  1±√12−4×1×(−1)  ＝ 1±√5  　　　　　2×1 　　2　 ４　比例定数a＝3×(−3)＝−9 　　したがってグラフは，第2第４象限の双曲線で，エ ５　(1)　ウ 　　(2)　√22+22＋22＝√4×3＝√12＝2√3 　　(3)　(1/3)×正方形ＡＢＦＥ×高さ 　　　　＝   1 ×22×2＝  8  3  3 じゃんけん  たくみ  グ  チ  パ  ゆり  グ  −  ゆ  た  チ  た  −  ゆ  パ  ゆ  た  − ６　勝敗表は右図で， 　勝ち負けが決まるのは 　　　　　　９通り中の６通り 　よって，6/9＝2/3	24三重県	【前期】 １　−8−2×(−9)＝−8＋18＝10 ２ 　4x−12y−6x＋3y ＝  −2x−9y 　　　　　　12　 　  　　12　 ３　上式×3＋下式×2より，23x＝69で，x＝3 　　これを上式に代入して，x＝3，y＝−3 ４　2√5＋ 　7√5 −5√5 ＝−  8√5 √5√5   　5　 ５　x＋5＝Ａとおくと， 　与式＝Ａ2＋3Ａ−4＝(Ａ＋4)(Ａ−1) 　　　　＝(x＋5＋4)(x＋5−1)＝(x＋9)(x＋4) 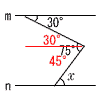６　右図のように平行線を入れる。 　　　∠x＝45°(錯角) ７　ＢＣ＝xとすると， 　　　長方形ＡＢＣＤ＝1×x＝x 　　　正方形ＥＣＦＧ＝(x−1)2 　　x＝(x−1)2より，x2−3x＋1＝0 　　x＞0だから，解の公式より， 　　x＝ 3＋√9−4 ＝ 3＋√5  　cm  　　　2　　 　　2　 【後期】 １　−42　　　２　−(9/12)−(2/12)＝−(11/12) ３　与式＝(a＋b)2＝(5−1)2＝42＝16 ４　2a＋6b−3a＋6b＝−a＋12b ５　5＋6√10−14＝−9＋6√10 ６　解の公式より， 　　　x＝−1±√1＋1＝−1±√2 ７　8÷40＝0.2