全国公立高校入試 　１番問題　【平成２６年春】

（６）宮城県

学習日　　　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

【　前　期　】		【　後　期　】
１	5−19＋7　　　　　　　　　　　　　　　　　 . .	１	6−2×(−5)　　　　　　　　　　　　　　　　　 .
２	−  7  ＋  3  ×(−2)　　　　　　　　　　　 .  2  4	２	1  −  7  　　　　　　　　　　　　　　　　　　　　　 .  　　3  9
３	Ａ＝3x＋1，Ｂ＝x−1として，Ａ−2Ｂを計算しなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	３	2(a＋3b)−(a−4b) 　　　　　　　　　　　　　　　　　　　　　　　　　 .
４	10x3y÷5xy2　　　　　　　　　　　　　　　　　　 .	４	√8＋ 　6 .   　　　　　　　　　　　　　　　　　 . √2
５	a2＋4a＋3　を因数分解しなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	５	２次方程式　x2＋2x−15＝0　を解きなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
６	２次方程式　x2＋5x＋2＝0　を解きなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	６	先端の色がそれぞれ赤，白，青である３本の棒があり，先端が見えない状態で箱の中に入っています。　この３本の棒をよく混ぜて１本取り出し，先端の色を確認してからもとにもどします。　このことを２回行うとき，確認した色が２回とも赤か，２回とも白になる確率を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 .
７	階級(分)   相対度数 以上　未満 　0〜　5   0.01 　　5〜　10   0.05  　10〜15  0.18 　15〜20  0.32  　20〜25  0.22  　25〜30  0.12  　30〜35  0.09  　35〜40 0.03  計 1.00 　右の表は，ある中学校で生徒の通学にかかる時間を調べ，相対度数を求めて表に整理したものです。　通学にかかる時間が25分以上となる生徒は，全体の何％ですか。 　　　　　　　　　　　　　　　　 .	７	相似な２つの立体Ｐ，Ｑがあり，その表面積の比は4：9です。　立体Pの体積が8cm3 のとき，立体Ｑの体積を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
		８	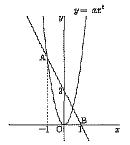右の図のように，関数 y＝ax2 のグラフ上に，x座標が−1となる点Ａをとります。また，x軸上の，座標が（1，0）となる点をＢとします。　直線ＡＢの切片が2のとき，aの値を求めなさい。 　　　　　　　　　　　　　　　　　 .
８	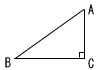右の図のような，∠ＡＣＢ＝90°の直角三角形ＡＢＣがあります。ＡＢ＝3cm，BC=2AC となるとき，辺ACの長さを求めなさい。 　　　　　　　　　　　　　　　　　　　 .	９	下の図のように，直線l と，２点Ａ，Ｂがあります。直線l 上にあって，２点Ａ，Ｂから等しい距離にある点Ｐを，作図によって求めなさい。　作図は，解答用紙の図に行い，点Ｐの位置を示す文字Ｐも書きなさい。　なお，作図に用いた線は消さずに残しなさい。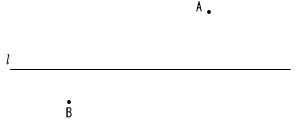
９	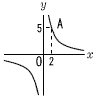yはxに反比例し，そのグラフは右の図のように点Ａ（2，5）を通ります。　x の変域が 1≦x≦5 のときのyの変域を求めなさい。 　　　　　　　　　　　　　　　　　 .