２６年山形県

～印刷して、紙の上でやってネ！（文字サイズを小にするとＡ４に収まります）～

１

(1)　

　1＋(－8)－6

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　

５

【選択問題】
　下の図は，数学の授業で学んだ立体を投影図に表したものである。　(Ａ)，(Ｂ)のどちらか１つを選び，その投影図で表された立体の体積を求めなさい。　なお，円周率はπとし，選んだ投影図の記号を解答欄に書くこと。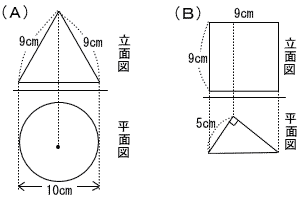

立面図は二等辺三角形　　　　立面図は正方形
平面図は円　　　　　　　　　　　平面図は直角三角形

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　

(2)　－	6	×(	1	－	1	)
	5		3		4

(3)　4ab²÷(－3b²)×6a

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　

(4)　√6(√3－4)＋√24

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　

２

　3x²y－6xy－24y　を因数分解しなさい。　途中の計算式も書くこと。　

　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　

３

　２次方程式　(3x＋4)(x－2)＝6x－9　を解きなさい。　解き方も書くこと。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　

６

　図１のように，直線l 上に２点Ａ，Ｂがある。　美咲さんは，次の［条件］の(1)，(2)をともにみたす点Ｐを作図しようとした。
　図２は，美咲さんが途中まで作図した状態を表している。　美咲さんが作図しようとした点Ｐを，定規とコンパスを使って，図２に作図しなさい。
　ただし，作図に使った線は残しておくこと。

［条件］

(1)	点Ｐは，直線l の上側にあり，∠ＰＡＢ＝30°である。
(2)	点Ｐを中心としたある円は，点Ｂで直線l に接する。

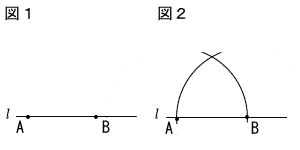４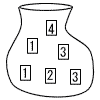

　右の図のように，袋の中に，数字の1，1，2，3，3，4 をそれぞれ１つずつ書いた６枚のカードが入っている。　この袋からカーを１枚取り出し，それを袋にもどしてかき混ぜ，また１枚取り出す。　このとき，少なくとも１回は，偶数を書いたカードが出る確率を求めなさい。
　ただし，どのカードが取り出されることも同様に確からしいものとする。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　