全国公立高校入試 　１番問題　【平成２５年春】		正　答　２
		９　栃木県　〜　１６　富山県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

９栃木県	１　−7　　　２　. 8ａ2ｂ×ａｂ ＝4ａ3ｂ2  　　　2　　 ３　. 3ｘ−1＋2ｘ ＝ 5ｘ−1  　　　4　　  　4　 ４　9−ｘ2 ５　３つの三角形に分けて， 　　　　180×3＝540° ６　. 　2×√6 . ＝ 2 √6＝ √6  √6×√6 6 　3 ７　ｙ＝ａｘに，ｘ＝−2，ｙ＝6を代入すると， 　　　　6＝−2ａより，ａ＝−3（比例定数） 　　よって，ｙ＝−3ｘ ８　解の公式より，ｘ＝ -(-3)±√(-3)2-4×１×1  　　　　　　2×1　　　　　　 　　　　ｘ＝ 3±√9−4 ＝ 3±√5  　　2　　  　2　 ９　出方（500円，100円）は，次の４通り 　　　(表，表）　（表，裏）　（裏，表）　(裏，裏） 　　よって，   2  ＝  1  4  2 10　上式−下式より，5ｙ＝−5で，ｙ＝−1 　　　これを上式に代入して，ｘ−2＝2で，ｘ＝4 　　　　　よって，ｘ＝4ｙ＝−1 11　5ｘ＋6ｙ＜1000 12　15人の中央値は8人目で，４点 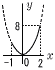13　右図参照 　　　ｘ＝2のとき，ｙ＝2×22＝8 　　　ｘ＝0のとき，ｙ＝2×02＝0 　　　　　よって，0≦ｙ≦8 14　面積比は，12：32＝1：9だから，９倍	13 東京都	１　−7−2＝−9 ２　9ａ＋9ｂ−ａ−3ｂ＝8ａ＋6ｂ ３　(√7)2＋4√7−12＝7＋4√7−12＝4√7−5 ４　ｘ−3ｘ＝1＋5 より，−2ｘ＝6 で，ｘ＝−3 ５　上式−下式×4より， 　　　23ｙ＝−23 で，ｙ＝−1 　　これを上式に代入して， 　　　4ｘ−(−1)＝9 より，ｘ＝2，ｙ＝−1 ６　(ｘ−5)(ｘ−7)＝0 より，ｘ＝5，7 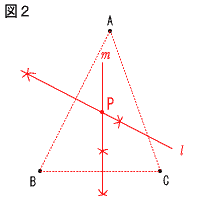７　26ｍ以上は4＋3＝7人だから，   7 ×100＝35％  20 ８　∠ＡＯＣ＝180× 4 ＝80°より，∠ＡＢＣ＝40° 9 　　∠ＢＯＤ＝180× 1 ＝60°より，∠ＢＡＤ＝30° 3 　　よって，∠ＡＥＣ＝40＋30＝70° ９　（右図参照） 　△ＡＢＣの外心を 　　　　　求めればよい。 　(ｉ)　辺ＡＢの垂直 　　　　二等分線を引く 　(ii)　辺BCの垂直 　　　　二等分線ｍを引く 　(iii)　とｍの交点Pを 　　　　作図する
10 群馬県	１　(1)　−5　　(2)　2＋6＝8　　(3)　2ａｂ ２　(−6)2＝36，−62＝−36だから，　＞ ３　ｘ2−(2ｙ)2＝ｘ2−4ｙ2 ４　(ｘ＋4)(ｘ−2) ５　与式＝ｘ(ｘ＋ｙ)＝√2（√2＋√3−√2) 　　　　　＝√2×√3＝√6 ６　両辺×2より，ｘ＋6＝4ｘ 　　　　3ｘ＝6で，ｘ＝2 ７　上式×3＋下式より，13ｘ＝39で，ｘ＝3 　　これを上式に代入して，12＋ｙ＝8で，ｙ＝−4 　　　　よって，ｘ＝3，ｙ＝−4 ８　∠ＡＣＢ＝∠ＡＤＢ＝36°（円周角） 　　∠ＡＢＣ＝90°（直径の円周角） 　　△ＡＢＣで，∠ＢＡＣ＝180−(36＋90)ー54° ９　条件に合うのは，右下表の14通り １回目 ２回目  １ １   ２ １，２  ３ １，３  ４ １，２，４   ５ １，５   ６ １，２，３，６  　　　　よって，  14  ＝  7 .  36  18 10　下図参照 　［作図法］ 　　対角線ACの垂直二等分線 　　を引き，交点をE，Fとする。 　［ひし形の性質］ 　　対角線が，それぞれの中点 　　で垂直に交わる。	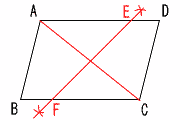14 神奈川県	１　4＋6＝10 ２　. −10＋6 ＝−  4  　　15　 15  ３　8ａ ４　. 　35×√7. −2√7＝ 5√7−2√7＝3√7 √7×√7 【２番おまけ】 １　ｘ2＋2ｘ−15−ｘ2＋4ｘ−4＝6ｘ−19 ２　ｘ2＋7ｘ−8＝(ｘ＋8)(ｘ−1) ３　解の公式より， 　　ｘ＝  −(−1)±√(−1)2−4×3×(−1)  　　　　　　　　2×3　　　　　 　　　＝  1±√1＋12 ＝  1±√13  　　　6　  　　6　　 ４　上式−下式×2より， 　　　5ｙ＝−10 で，ｙ＝−2 　　これを下式に代入して， 　　　2ｘ−(−2)＝8 より，ｘ＝3，ｙ＝−2 　＜以下，省略＞
11 埼玉県	１　8ｘ　 ２　9−2＝7　 ３　4√2＋5√2＝9√2 ４　与式＝(ｘ−1)2＝(√5＋1−1)2＝(√5)2＝5 ５　解の公式より， 　　ｘ＝ −3±√32−4×2×(−4) ＝ −3±√41  　　　　　　2×2  　　4 ６　上式−下式×2より，ｙ＝−5 　　これを下式に代入して，2ｘ−5＝3 　　　よって，ｘ＝4，ｙ＝−5 ７　変化の割合＝ 32ａ−12ａ ＝ 8ａ ＝4ａ＝2  　3−1  2 　　　よって，ａ＝ 1 2 ８　1.95≦   ｎ ＜2.05 より，78≦ｎ＜82 40 　　　よって，最小のｎ＝78 ９　２点ＡとＢは原点対称だから， 　　　Ａ(−2，3)，Ｂ(2，−3)となる。 　　式に(−2，3)を代入して，3＝ 　ａ . 　より，  −2 　　　　ａ＝−6 10　（右図参照） 　底面の円周は6πcmだから， 　　32π×2＋5×6π＝18π＋30π 　　＝48πcm2　 　　＜11は省略＞	15 新潟県	１　−8　　　２　9ａ−6ｂ−4ａ＋4ｂ＝5ａ−2ｂ ３　12ａ6÷4ａ3＝3ａ3 ４　上式＋下式×2より， 　　　　7ｘ＋6ｘ＝12＋14で，ｘ＝2 　　これを上式に代入して， 　　　　14＋2ｙ＝12で，ｙ＝−1 　　よって，ｘ＝2，ｙ＝−1 ５　(ｘ＋5)(ｘ−6) ６　√3−2√3＝−√3 ７　解の公式より，ｘ＝ −6±√62−4×1×7 　　　　　　2×1　　　　 　　　　＝ −6±√36−28 ＝ −6±2√3  　　　　2　　　　  　　　2　　 　　　　＝−3±√3 ８　ｙ＝  ａ 　に，ｘ＝3，ｙ＝3を代入すると，  ｘ 　　　　3＝   ａ 　より，ａ＝9（比例定数）   3 　　よって，ｙ＝  9  ｘ ９　相似比は2：3だから， 　　　　体積比は，23：33＝8：27 10　∠ｘ＝180°−∠Ｃ＋∠Ｄ＝180°−∠Ｂ−∠Ｄ 　　　　　＝180°−68°−32°＝80° 11　（省略） 12　鯉の総数を ｘ 匹とすると， 　　　　. 60 ＝  9 より，ｘ＝3600÷9≒400匹 ｘ 60
12 千葉県	【前期】 １　7＋5＝12　　　２　16−6＝10 ３　. 6ｘ−24ｙ − 3ｘ−8ｙ ＝ 6ｘ−24ｙ−3ｘ＋8ｙ  　　4　  　4　  　　　　4 　　＝ 3ｘ−16ｙ  　　または，  3 ｘ−4ｙ  　　4　  4 ４　5(ｘ−2)＝2(ｘ＋7) より，3ｘ＝24で，ｘ＝8 ５　3√5−2√5＋ 　15×√5 ＝4√5 √5×√5 ６　ｘ2-6ｘ-7-20＝ｘ2-6ｘ-27＝(ｘ−9)(ｘ＋3) 　　【後期】 １　7−9＝−2 ２　8×  9  ＝18  4 ３　6ａ−3ｂ−ａ＋3ｂ＝5ａ ４　外角の和より，１つの外角は360÷10＝36° 　　　　よって，180−36＝144° ５　2×5−√15＋2√15−3＝7＋√15 ６　解の公式より，ｘ＝ -(-3)±√(-3)2-4×１×(-1)  　　　　　　2×1　　　　　　 　　　　ｘ＝ 3±√9＋4 ＝ 3±√13  　　2　　  　2	16 富山県	１　7−27＝−20 ２　4√3＋√3−2√3＝3√3 ３　2ａ＋3−3ａ＋18＝−ａ＋21 ４　与式＝(2ｘ＋ｙ)(2ｘ−ｙ)＝4×8＝32 ５　(ｘ−6)(ｘ＋4)＝0　より，ｘ＝6，−4 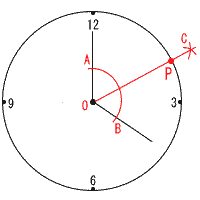６　200×(1＋ 　ａ　. ＝200＋2ａ　(ｇ)  100  ７　(ｘ，ｙ)＝(1，6)　(2，3)　(3，2)　(6，1)　の４通り 　よって，求める確率＝   4  ＝  1 36   9 8　（右図参照） 　長針と短針の間の角（120°）の２等分線を作図すればよい。 　(1)　中心Ｏから弧ＡＢをとる 　(2)　ＡとＢから等距離に点Ｃ 　　　をとる 　(3)　線分ＯＣと円周の交点Ｐ 　　　が，求める点 　［別解］　12時の点から，円周上に半径と等しい距離 　　　　　　をとる