|
(29) 奈良県 | 学習日 月 日( ) |
|
(29) 奈良県 | 学習日 月 日( ) |
〜 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)〜
| 1 | (1) . |
6 | 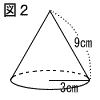 図2は,底面の半径が3cm,母線の長さが9cmの円すいである。 この円すいの体積を求めよ。 ただし,円周率はπとする。 図2は,底面の半径が3cm,母線の長さが9cmの円すいである。 この円すいの体積を求めよ。 ただし,円周率はπとする。. |
||||||
| (2) . |
|||||||||
| (3) x y2×6y÷3x y . |
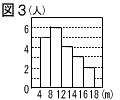 図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,平均値は12.2mであった。 このヒストグラムから読み取れることについて述べた次のア〜エのうち,正しいものをすべて選び,その記号を書け。 図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,平均値は12.2mであった。 このヒストグラムから読み取れることについて述べた次のア〜エのうち,正しいものをすべて選び,その記号を書け。
. |
||||||||
| 7 | |||||||||
| (4) (x−7)(x−4)+8x . |
|||||||||
| 2 | 1次方程式 x+4=5(2x−1) を解け。 . |
||||||||
| 3 | 2次方程式 x2+3x−18=0 を解け。 . |
8 | 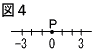 図4で,数直線上を動く点Pは,最初,原点Oにある。 点Pは,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,裏が出れば負の方向に1だけ移動する。 硬貨を3回投げて移動した結果,点Pが原点にある確率を求めよ。 図4で,数直線上を動く点Pは,最初,原点Oにある。 点Pは,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,裏が出れば負の方向に1だけ移動する。 硬貨を3回投げて移動した結果,点Pが原点にある確率を求めよ。. |
||||||
| 4 |
. |
9 | 図5のような正方形ABCDの紙がある。 辺ABが対角線ACに重なるように紙を折ったときの折り目と辺BCの交点をEとする。 点Eを,定規とコンパスを使って下の枠内に作図せよ。 なお,作図に使った線は消さずに残しておくこと。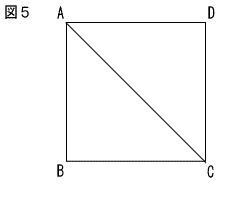 |
||||||
| 5 | 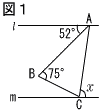 図1で,2直線 図1で,2直線. |
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |