|
(25) 滋賀県 | 学習日 月 日( ) |
|
(25) 滋賀県 | 学習日 月 日( ) |
~ 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)~
| 1 | 3 |
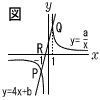 グラフが2点P,Qで交わっている。 グラフが2点P,Qで交わっている。y=4x+bのグラフとx軸との交点Rのx座標は-1,交点Qのx座標が1であるとき,aの値を求めなさい。 |
||||||
|
||||||||
| 4 | ||||||||
| (4) 10xy2÷5y×(-x)2 |
||||||||
| (5) (√3+5) (√3-1)+√12 |
5 | 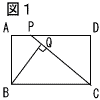 (1) 図1のように,長方形ABCDの辺AD上に点Pをとり,BQ⊥CPとなる線分CP上の点をQとする。このとき,△BCQ∽△CPDを証明しなさい。 (1) 図1のように,長方形ABCDの辺AD上に点Pをとり,BQ⊥CPとなる線分CP上の点をQとする。このとき,△BCQ∽△CPDを証明しなさい。【証明】 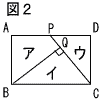 (2) 図2のように,BQ=CP,BQ⊥CPであるとき,長方形ABCDをア,イ,ウの3つの図形に分けて,それらを並べかえると,図3のようなB BQ,CPと同じ長さの線分を1辺とする正方形ができる。 図3の正方形に線を書き入れ,ア,イ,ウのそれぞれ 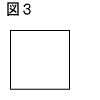 がどこにおさまるか示しなさい。 がどこにおさまるか示しなさい。 |
||||||
| 2 | 次の2次方程式を解きなさい。 x2-3x+1=0 |
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |