|
正 答 2 | ||||
| 9栃木県 〜 16富山県 | |||||
|
正 答 2 | ||||
| 9栃木県 〜 16富山県 | |||||
| 9栃木県 |
5 比例定数a=x y=(−6)×(−2)=12より, 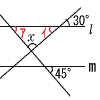
∠ア=45°(同位角) ∠イ=30°(対頂角) ∠x=180−(∠ア=∠イ) =180−(45+30)=105° 7 3a=b+4cより,
x=2のとき,y=−2+3=1 よって,1≦y≦6 10 (2+10+8+x+7)÷5=6より, x+27=30で,x=3 11 底面積=62=36 側面積=(1/2×6×8)×4=96 よって,36+96=132cm2
△OAMで,AM2+32=42より, AM=√7だから,AB=2√7cm 14 √3n=√3×(3×2×2) すなわち,n=3×2×2=12 |
13東京都 | 1 6−2=4 2 8a+b−a+7b=7a+8b 3 (√5)2−(√3)2=5−3=2 4 9x−8x=8−2より,x=6 5 下式−上式×2より,3y=−15で,y=−5 これを上式に代入して,3x−5=4より,x=3 よって,x=3,y=−5 6 (x−9)(x+1)=0より,x=9,−1
8 6個から2個取り出す方法は,6×5÷2=15通り 赤玉2個から1個取り出す方法は,2通り 白玉4個から1個取り出す方法は,4通り よって,2×4÷15
9 ∠ABCの二等分線とACの交点が点P 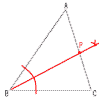 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10群馬県 | 1 4 2 7.5a
〜2番問題 (おまけ)〜 1 −1.98<x<2.25より,x=−1,0,1,2 2 与式=x2−x−12−8=x2−x−20 =(x−5)(x+4) 3 x2+2x−5=0で,解の公式より,
|
14神奈川県 | 1 −3 2 6−3×(−4)=6+12=18
〜2番問題 (おまけ)〜 1 x2−3x−18−4x=x2−7x−18=(x−9)(x+2) 2 解の公式より,
x=3のとき,y=−1/3×32=−3 よって,−3≦y≦0より,a=−3,b=0
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11埼玉県 | 1 6y 2 −12+7=−5 3 3√3−√3=2√3 4 与式=(x−7)(x+4)=(16−7)×(16+4) =9×20=180 5 解の公式より,
これを上式に代入して,x+2=5 よって,x=3,y=1 7 x=−2のとき,y=−1/2×(−2)2=−2 x=1のとき,y=−1/2×12=−1/2 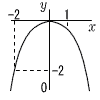 よって,−2≦y≦0 よって,−2≦y≦08 半径3cmの半球となるから,
9 ∠AOB(外側)=2x=360−x 3x=360より,x=120° 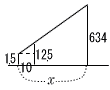 10 (右図参照) 10 (右図参照)新タワーまでx mとすると, 10:x=(12.5-1.5):(634-1.5) 11x=6325より,x=575m 11 ア 平均値=(6+5+・・・+6)÷12 =8.5回 中央値は6番目(5回)と7番目(6回)の平均値で, (5+6)÷2=5.5回 イ Tさんは上位から3番目で,できる方になる。 中央値がふさわしい。 |
15新潟県 |
4 2a2×9b2×(−ab2)=−18a3b4 5 45:横=3:4より,横=45×4÷3=60cm 6 上式−下式×2より,7y=−7で,y=−1 これを下式に代入して,x+5=8 よって,x=3,y=−1 7 √18+√2=3√2+√2=4√2 8 解の公式より,
これをy=ax2に代入すると, 1=a×22より,a=1/4 10 x :8=1:2より,x=4 8:(y+4)=1:2より,y+4=16 よって,x=4,y=12 11 ∠x=360−∠BOC=360−70×2 =360−140=220° 12 表にまとめると,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12千葉県 | [前期] 1 8 2 8−25×2/5=8−10=−2 3 2a+4b−3a+3b=−a+7b 4 y=−2(x−1)+3より,y=−2x+5 5 6−√3+4√3−2=4+3√3 6 解の公式より,
[後期] 1 15 2 2−3=−1 3 8x−20−3=3x+2 5x=25より,x=5
|
16富山県 | 1 6−3=3 2 3a+6+2a−8=5a−2 3 両辺×2より,2x=x−6 よって, x=−6
点Aから垂線を引き, 8 底面の円周は8πcmだから, 側面の扇形の弧の長さも8πcm 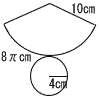 よって,側面積(扇形)は, よって,側面積(扇形)は,
42π=16πcm2 よって表面積は, 40π+16π=56πcm2 9 エ 10 すべての場合は33=27通り このうち,Aだけが勝つのは3通り
|
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] |