全国公立高校入試
　１番問題　【平成２４年春】
（２９）　奈良県 　学習日　　　 　　 月　　 　　日（　　　　）
〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜
［　特　　色　］ ［　一　　般　］
１ 　(1)　−9＋5
　　　　　　　　　　　　　　　　　　　　　　　　　 .
(2)　8ｘ−3ｙ＋2ｘ−6ｙ
　　　　　　　　　　　　　　　　　　　　　　　　　 .
(3)　6ａｂ2÷3ａｂ
　　　　　　　　　　　　　　　　　　　　　　　　　 .
(4)　(ｘ＋1)2−8
　　　　　　　　　　　　　　　　　　　　　　　　　 .
(5)　√27＋√3
　　　　　　　　　　　　　　　　　　　　　　　　　 .		 １ (1)　6×(−7)
　　　　　　　　　　　　　　　　　　　　　　　　　 .
(2)　5ｘ−4(ｘ−2ｙ)
　　　　　　　　　　　　　　　　　　　　　　　　　 .
(3)　ａ×6ａｂ÷2ａ2

　　　　　　　　　　　　　　　　　　　　　　　　　 .
(4)　(ｘ−3ｙ)2＋8ｘｙ

　　　　　　　　　　　　　　　　　　　　　　　　　 .　
２ 　１次方程式　3ｘ−5＝ｘ＋9　を解け。

　　　　　　　　　　　　　　　　　　　　　　　　　 .		 ２
− 7 より大きく，√11より小さい整数は何個あるか。
3
　　　　　　　　　　　　　　　　　　　　　　　　　 .　　　
３ 　２次方程式　ｘ2−4ｘ−12＝0　を解け。

　　　　　　　　　　　　　　　　　　　　　　　　　 .		 3
連立方程式　｛ . ｘ＋3ｙ＝1 　を解け。
2ｘ−ｙ＝9
　　　　　　　　　　　　　　　　　　　　　　　　　 .
４ 　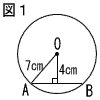図１で，２点Ａ，Ｂは半径が7cmである円Ｏの周上にあり，中心Ｏから弦ＡＢまでの距離は4cmである。弦ＡＢの長さを求めよ。


　　　　　　　　　　　　　　　　　　　　　 .　　		 ４ 　２次方程式　ｘ2−5ｘ＝6　を解け。




　　　　　　　　　　　　　　　　　　　　　　　　　 .
５ 　Ａ，Ｂ，Ｃ，Ｄ，Ｅの５人から２人の当番をくじで選ぶとき，Ａが当番に選ばれる確率を求めよ。



　　　　　　　　　　　　　　　　　　　　　　　　　 .		 ５ 　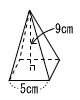右の図は，底面の１辺の長さが5cmで，高さが9cmの正四角すいである。この正四角すいの体積を求めよ。


　　　　　　　　　　　　　　　　　　　　　　　 .
６ 　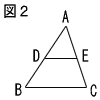図２の△ＡＢＣで，点Ｄは辺ＡＢの中点であり，点Ｄを通り辺ＢＣに平行な直線と辺ＡＣとの交点をとする。
(1)　点Ｄを，定規とコンパスを使って解答欄の枠内に作図せよ。なお，作図に使った線は消さずに残しておくこと。
　　　［解答欄は右下］
(2)　△ＡＢＣの面積が24cm2のとき，△ＡＤＥの面積を求めよ。
　　　　　　　　　　　　　　　　　　　　　　　　　 .　　		 ６ 　袋の中に白の碁石だけだ入っている。黒の碁石100個をその袋の中に入れ，よくかき混ぜた後，その袋の中から80個の碁石を無作為に抽出して調べたら，黒の碁石が10個ふくまれていた。抽出する前の袋の中には，およそ何個の白の碁石が入っていたと考えられるか。次のア〜エのうち，適切なものを１つ選び，その記号を書け。
　ア　およそ700個　　　　イ　およそ800個
　ウ　およそ900個，　　　エ　およそ1000個

　　　　　　　　　　　　　　　　　　　　　　　　　 .
７ 　ある道のりを毎分60mの速さで歩いたところ，20分かかった。同じ道のりを，自転車に乗って毎分ｘmの速さで走るときにかかる時間をｙ分として，次の(1)，(2)の問いに答えよ。ただし，ｘは正の数とする。
(1)　ｘの値とそれに対応するｙの値の関係として適切なものを，次のア〜エから１つ選び，その記号を書け。
　ア　ｘの値とｙの値の和は，一定である。
　イ　ｙの値からｘの値を引いたときの差は，一定である。
　ウ　ｘの値とｙの値の積は，一定である。
　エ　ｙの値をｘの値で割った商は，一定である。
　　　　　　　　　　　　　　　　　　　　　　　　　 .
(2)　ｙ をｘ の式で表せ。
　　　　　　　　　　　　　　　　　　　　　　　　　 .		 　［特色６番の解答欄］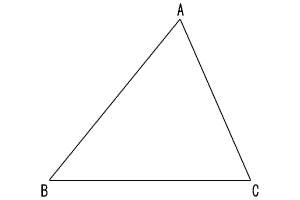
［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい