|
(3) 秋田県 | 学習日 月 日( ) |
|
(3) 秋田県 | 学習日 月 日( ) |
| 次の 1 〜 15 の中から,指示された 8問 について答えなさい。 | |||||||||||
| 1 | . . |
9 | ある中学校の昨年度の生徒数は230人であった。今年度の生徒数は,昨年度と比べ,男子が10%増え,女子が5%減り,全体で5人増えた。昨年度の男子,女子それぞれの生徒数を求めなさい。 . |
||||||||
| 2 | 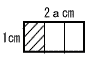 右の図のように,縦1cm,横2acmの長方形の板が3等分されている。このとき,図の斜線部分の面積を,aを用いた式で表しなさい。 右の図のように,縦1cm,横2acmの長方形の板が3等分されている。このとき,図の斜線部分の面積を,aを用いた式で表しなさい。. |
10 | . |
||||||||
| 3 | 2a+b から 3a−b をひいた差を求めなさい。 . |
11 | 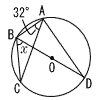 右の図のように,円Oの周上に4点A,B,C,Dがあり,線分BDは直径である。∠BAC=32°のとき,∠xの大きさを求めなさい。 右の図のように,円Oの周上に4点A,B,C,Dがあり,線分BDは直径である。∠BAC=32°のとき,∠xの大きさを求めなさい。. |
||||||||
| 4 |
. |
12 |  . |
||||||||
| 5 |
|
||||||||||
| 6 |
. |
13 | 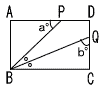 右の図で,四角形ABCDは長方形である。点Pは辺AD上の点であり,∠PBCの二等分線と辺CDの交点をQとする。∠APB=a°,∠BQC=b°とするとき,bをaを用いた式で表しなさい。 右の図で,四角形ABCDは長方形である。点Pは辺AD上の点であり,∠PBCの二等分線と辺CDの交点をQとする。∠APB=a°,∠BQC=b°とするとき,bをaを用いた式で表しなさい。. |
||||||||
| 7 | 次の方程式ア,イを解きなさい。 ア (x−2)(x+2)=3x . イ 2x2−5x−1=0 . |
14 | 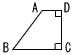 右の図のように,台形ABCDがあり,AD=1cm,CD=2cm,∠BCD=∠ADC=90°,∠BAD=135°である。この台形ABCDを辺CDを軸として1回転してできる立体の体積を求めなさい。ただし,円周率をπとする。 右の図のように,台形ABCDがあり,AD=1cm,CD=2cm,∠BCD=∠ADC=90°,∠BAD=135°である。この台形ABCDを辺CDを軸として1回転してできる立体の体積を求めなさい。ただし,円周率をπとする。. |
||||||||
| 8 | 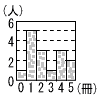 右の図は,あるクラスの15人が冬休みに読んだ本の冊数を,ヒストグラムに表したものである。この15人が読んだ本の冊数について,次のア〜エから正しいものを1つ選んで記号を書きなさい。 右の図は,あるクラスの15人が冬休みに読んだ本の冊数を,ヒストグラムに表したものである。この15人が読んだ本の冊数について,次のア〜エから正しいものを1つ選んで記号を書きなさい。
. |
15 | 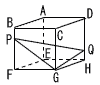 . |
||||||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |