|
(3) 秋田県 | 学習日 月 日( ) |
|
(3) 秋田県 | 学習日 月 日( ) |
〜 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)〜
| 次の1〜15の中から,指示された8問について答えなさい。 | |||||||||||||
| 1 | ア 2+(−3) イ 2−(−3) ウ 2×(−3) エ 2÷(−3) . |
8 |
. |
||||||||||
| 2 | 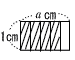 右の図のように,縦1cm,横acmの長方形の板が5等分されている。このとき,図の斜線部分の面積を,aを用いた式で表しなさい。 右の図のように,縦1cm,横acmの長方形の板が5等分されている。このとき,図の斜線部分の面積を,aを用いた式で表しなさい。. |
9 | 定価a円の25%引きの値段のついた商品が,さらに50円引きで売られている。この商品を1個買ったときの代金を,aを用いた式で表しなさい。 . |
||||||||||
| 3 |
. |
10 | . |
||||||||||
| 4 |
. |
11 | 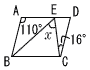 右の図において,四角形ABCDは平行四辺形である。点Eは辺AD上の点であり,AB=AE,∠BAE=110°,∠ECD=16°である。このとき,∠xの大きさを求めなさい。 右の図において,四角形ABCDは平行四辺形である。点Eは辺AD上の点であり,AB=AE,∠BAE=110°,∠ECD=16°である。このとき,∠xの大きさを求めなさい。. |
||||||||||
| 5 | 次のア〜オから,正しくないものを1つ選んで記号を書きなさい。
|
12 | 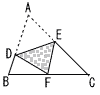 右の図のように,周の長さが22cmである△ABCがある。点Aが辺BC上にくるように辺AB,AC上の点D,Eを結ぶ線分を折り目として折り返し,点Aが辺BCと重なる点をFとする。BC=8cm,DB=2cm,EF=3cmのとき,線分DFと線分ECの長さの和を求めなさい。 . 右の図のように,周の長さが22cmである△ABCがある。点Aが辺BC上にくるように辺AB,AC上の点D,Eを結ぶ線分を折り目として折り返し,点Aが辺BCと重なる点をFとする。BC=8cm,DB=2cm,EF=3cmのとき,線分DFと線分ECの長さの和を求めなさい。 . |
||||||||||
| 13 | 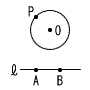 右の図のように,点Oを中心とする円と直線がある。直線上に2点A,Bがある。円の半径は4cm,点Oと直線の距離は6cm,AB=5cmである。円周上を動く点Pと2点A,Bを結んでできる△PABの面積の,最も大きな値と最も小さな値の差を求めなさい。 右の図のように,点Oを中心とする円と直線がある。直線上に2点A,Bがある。円の半径は4cm,点Oと直線の距離は6cm,AB=5cmである。円周上を動く点Pと2点A,Bを結んでできる△PABの面積の,最も大きな値と最も小さな値の差を求めなさい。. |
||||||||||||
| 6 | √3=1.732として,6÷√3 の値を求めるために,学さんはa×1.732と計算した。この計算が正しくなるようなaの値を求めなさい。 . |
14 | 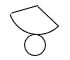 右の図は,円すいの展開図である。底面の半径は3cm,側面のおうぎ形の中心角は120°である。この展開図を組み立てたときにできる円すいの高さを求めなさい。 右の図は,円すいの展開図である。底面の半径は3cm,側面のおうぎ形の中心角は120°である。この展開図を組み立てたときにできる円すいの高さを求めなさい。. |
||||||||||
| 7 | xについての2次方程式 x(x+1)=a の解の1つは2である。このとき,次の(1),(2)の問いに答えなさい。 (1) aの値を求めなさい。 . (2) もう1つの解を求めなさい。 . |
15 | 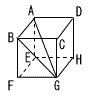 右の図のように,1辺が6cmの立方体ABCD−EFGHがある。この立方体の3つの頂点A,B,Gを結んでできる△ABGについて,次の(1),(2)の問いに答えなさい。 右の図のように,1辺が6cmの立方体ABCD−EFGHがある。この立方体の3つの頂点A,B,Gを結んでできる△ABGについて,次の(1),(2)の問いに答えなさい。(1) 辺AGを底辺としたときの高さを求めなさい。 . (2) 辺AGを軸として1回転してできる立体の体積を求めなさい。ただし,円周率をπとする。 . |
||||||||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |