|
(2) 青森県 | 学習日 月 日( ) |
|
(2) 青森県 | 学習日 月 日( ) |
〜 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)〜
| 前 期 | 後 期 | |||||||||||||||
| 1 | ア . イ . ウ .
|
1 | ア .
ウ . エ (x−4y)−(6x+5y) . オ 2√27−√12 . |
|||||||||||||
| 2 | 次の連立方程式を解きなさい。
|
2 | 次の等式をaについて時無し。 . |
|||||||||||||
| 3 | 次の二次方程式を解きなさい。 x2+4x−1=0 . |
3 |
. |
|||||||||||||
| 4 | 次の式を因数分解しなさい。 a2+8a−48 . |
4 | yはxの一次関数で,そのグラフが2点(−1,1),(3,9)を通るとき,この一次関数の式を求めなさい。 . |
|||||||||||||
| 5 | 
のグラフがある。点Aのx座標が6の とき,aの値を求めなさい。 |
5 | 二次方程式 x2−2x+a=0 の2つの解がx=−3,bであるとき,a,bの値を求めなさい。 . |
|||||||||||||
| 6 | 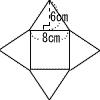 . |
6 | 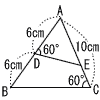 右の図のように,△ABCの辺AB,AC上にそれぞれ点D,Eをとるとき,AEの長さを求めなさい。 右の図のように,△ABCの辺AB,AC上にそれぞれ点D,Eをとるとき,AEの長さを求めなさい。. |
|||||||||||||
| 7 | 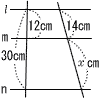 右の図で, 右の図で,. |
7 | 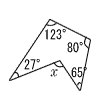 右の図の∠x の大きさを求めなさい。 右の図の∠x の大きさを求めなさい。. |
|||||||||||||
| 8 | 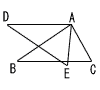 . |
8 | 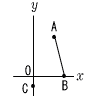 点Aの座標は(3,4),点Bの座標は(4,0),点Cの座標は(0,−1)である。点Cを通る直線の式を y=ax−1とする。この直線が線分AB(両端の点A,Bを含む)と交わるとき,aの値の範囲を求めなさい。 点Aの座標は(3,4),点Bの座標は(4,0),点Cの座標は(0,−1)である。点Cを通る直線の式を y=ax−1とする。この直線が線分AB(両端の点A,Bを含む)と交わるとき,aの値の範囲を求めなさい。. |
|||||||||||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |