|
惓丂摎丂係 | ||||
| 25丂帬夑導丂乣丂32丂搰崻導 | |||||
|
惓丂摎丂係 | ||||
| 25丂帬夑導丂乣丂32丂搰崻導 | |||||
| 25帬夑導 | 侾丂(1)丂亅4亄7亖3 丂丂(2)丂4倎亅2亄3倎亖7倎亅2
丂丂(5)丂併2亄2併2亖3併2 俀丂倶2亄倶亖2 丂丂(倶亄2)(倶亅1)亖0傛傝丆倶亖亅2丆1 俁丂32兾亊1亄1/3亊32兾亖1俀兾cm3 係丂敿墌偺屖乮捈宎乯偵懳偡傞墌廃妏偼90亱偩偐傜 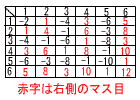 俆丂嘆丂(2丆3)丂(3丆2)丂(4丆5)丂(5丆4) 偺係捠傝 俆丂嘆丂(2丆3)丂(3丆2)丂(4丆5)丂(5丆4) 偺係捠傝丂丂嘇丂塃恾偺傛偆偵丆21捠傝 丂丂丂丂傛偭偰丆21/36亖7/12 |
29撧椙導 | 侾丂(1)丂亅28丂丂 丂(2)丂8倶亄5倷 丂丂(3)丂6倎2倐丂丂丂(4)丂倶2亄3倶倷亄倷2
俁丂忋幃亊2亅壓幃亊3傛傝丆 丂丂丂丂倶亖2丆倷亖3 係丂倶2亅2倶亅15亄3倶亖5 丂丂(倶亄5)(倶亅4)亖0傛傝丆倶亖亅5丆4 俆丂墶偼丆20亊4亅3倎亖80亅3倎偩偐傜丆 丂丂丂20亊2亄2(80亅3倎)亖200亅6倎丂(cm) 俇丂僀丆僂丆僄 丂 |
||||||||||||||||||||
| 26嫗搒晎導 | 侾丂亅18亅18亖亅36 俀丂3(2倎亅1)亅2(倎亅2)亖6倎亅3亅2倎亄4 丂丂丂丂亖4倎亄1 俁丂2併2亅3併2亖亅併2 係丂倶2亄4倶倷亄4倷2亅倶2亄倷2 丂丂丂亖4倶倷亄5倷2 俆丂倷愗曅偑亅1偱丆孹偒1/3偺捈慄乮塃壓恾乯 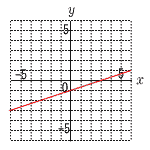 俇丂忋幃亊3亄壓幃亊2傛傝丆 俇丂忋幃亊3亄壓幃亊2傛傝丆丂丂丂丂13倶亖39偱丆倶亖3 丂丂偙傟傪壓幃偵戙擖偟偰丆 丂丂丂丂6亄3倷亖12偱丆倷亖2 丂丂傛偭偰丆倶亖3丆倷亖2 俈丂倶2亄36亖12倶傛傝丆 丂丂丂(倶亅6)2亖0偱丆倶亖6 |
30榓壧嶳導 | 侾丂(1)丂亅5
俀丂倶亅2亖亇4傛傝丆倶亖2亇4偱 丂丂倶亖6丆亅2 俁丂倎亖倶倷亖2亊4亖8 係丂佢倶亖360亊0.6亖216亱 俆丂倶2亄17倶亅18亖(倶亄18)(倶亅1) 丂丂倶2亄7倶亅18亖(倶亄9)(倶亅2) 丂丂倶2亄3倶亅18亖(倶亄6)(倶亅3)偑峫偊傜傟傞 丂丂傛偭偰丆(傾丆僀丆僂)亖(17丆18丆1) 丂丂丂丂丂丂丂丂丂(7丆9丆2)丂(3丆6丆3) 偺偄偢傟偐 |
||||||||||||||||||||
| 27戝嶃晎 | 乵屻婜俙乶 侾丂(1)丂8丂丂(2)丂2倎亅3倐丂丂(3)丂4倎2丂丂(4)丂2併3 俀丂椉曈亊4傛傝丆5倎亄倐亖2 丂丂丂丂傛偭偰丆倐亖2亅5倎 俁丂(3亄倶)(3亅倶) 係丂榓偑俉偲側傞偺偼師偺俆捠傝 丂丂丂(2,6)丂(3,5)丂(4,4)丂(5,3)丂(6,2) 丂丂傛偭偰丆5/36 俆丂俙偺倶嵗昗傪倎偲偡傞偲丆 丂丂丂丂仮俷俙俛亖1/2亊3亊倎亖4傛傝丆倎亖8/3 丂丂傛偭偰丆倷亖倎2亖64/9 俇丂傾丂倷亖40/倶丂乮斀斾椺乯 丂丂僀丂倷亖12倶丂乮斾椺乯 丂丂僂丂倷亖8/倶丂乮斀斾椺乯 丂丂僄丂倷亖倶/120丂乮斾椺乯 丂丂僆丂倷亖70亅倶丂乮侾師娭悢乯 丂丂傛偭偰丆僀丂僄 俈丂傾丂僂 俉丂僀丂僂 乵屻婜俛乶 侾丂5亅2亅6亖亅3
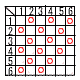 丂丂丂亖亅5倶2亄12倷亅13倷2 丂丂丂亖亅5倶2亄12倷亅13倷2係丂倎亖3丆5丆7丆9偩偐傜丆 丂丂丂塃偺傛偆偵16捠傝偵側傞 丂丂傛偭偰丆16/36亖4/9 俆丂僂 俇丂(1)丂俙丂倷亖1/8倲2 丂丂丂丂丂俢丂倷亖倎倶+2偵丆(倲丆亅2)傪戙擖 丂丂丂丂丂丂丂亅2亖倎倲亄2傛傝丆倎亖亅4/倲 丂丂丂丂丂丂丂倷亖(亅4/倲)倶亄2=0 丂丂丂丂丂丂丂亅4倶亄2倲亖0傛傝丆倶亖1/2倲 丂丂(2)丂倷亖(亅4/倲)倶亄2偵俤(亅8丆8)傪戙擖 丂丂丂丂丂丂8亖32/倲亄2傛傝丆倲亖16/3 |
31捁庢導 | 侾丂(1)丂亅2亄10亖亅8
俀丂倐(倎亄2) 俁丂(倶亅2)(倶亅5)亖0傛傝丆倶亖2丆5 係丂佢俛俤俢亖180亅65亊2亖50亱 丂丂佢俛俤俢亖佢俛俢俤亖50亱傛傝丆 丂丂丂丂佢倶亖180亅50亊2亖80亱 俆丂倷亖2(倶亅1)亄3偩偐傜丆 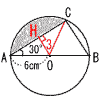 丂丂丂丂倷亖2倶亄1 丂丂丂丂倷亖2倶亄1
俈丂愵宍俷俙俠 丂丂丂亖62兾亊(120/360) 丂丂丂亖12兾cm2 丂丂俷俫亖3cm丆AC=6併3cm偩偐傜丆 丂丂丂丂仮俷俙俠亖1/2亊6併3亊3亖9併3cm2 丂丂傛偭偰丆12兾亅9併3丂cm2 俉丂乵徹柧乶 丂仮BDE偲仮CAE偵偍偄偰丆 丂丂佢BED=佢CEA乮嫟捠乯 丂丂佢DBE亖佢ACE乮屖AD偺墌廃妏乯 丂俀慻偺妏偑摍偟偄偐傜丆 丂丂仮BDE佷仮CAE 俋丂曈BC傪侾曈偲偡傞惓嶰妏宍傪偐偗偽傛偄 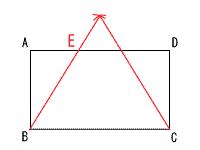 |
||||||||||||||||||||
| 28暫屔導 | 侾丂亅7亅3亖亅10
係丂(倶亄6)(倶亅2)亖0傛傝丆倶亖亅6丆2 俆丂捈宎偵懳偡傞墌廃妏偩偐傜丆佢俛俙俢亖90亱 丂丂佢俠亖佢俢亖50亱(屖俙俛偺墌廃妏) 丂丂傛偭偰丆佢倶亖180亅90亅50亖40亱 俇丂倎亖倶倷亖6亊(亅3)亖亅18 丂丂倷亖亅18/倶偵倷亖9傪戙擖偟偰丆 丂丂丂丂9亖亅18/倶傛傝丆倶亖亅2 俈丂嘆慄暘俙俛偺悅捈擇摍暘慄傪堷偔 丂丂嘇慄暘俛俠偺悅捈擇摍暘慄傪堷偔 丂丂嘊俀杮偺悅捈擇摍暘慄偺岎揰傪俷偲偡傞 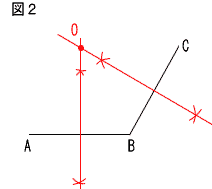 |
32搰崻導 | 侾丂15亄18亖33 俀丂2併3亄3併3亅4併3亖併3
丂丂倶亖亅4丆2 俇丂倷亖倎倶丂偵(6丆亅18)傪戙擖偡傞偲丆 丂丂亅18亖6倎偱丆倎亖亅3 丂傛偭偰丆倷亖亅3倶 俈丂懳愴慻崌傢偣偼師偺捠傝 丂俙俛丆俙俠丆俙俢丆俛俠丆俛俢丆俠俢 丂丂傛偭偰丆俇帋崌 俉丂俙俠偱慄懳徧傛傝丆俙俛亖俙俢丆CB亖CD 丂丂俛俢偱慄懳徧傛傝丆AB亖CB丆AD亖CD 丂丂丂傛偭偰丆係曈偺挿偝偡傋偰偑摍偟偄 丂丂傑偨丆佢BAD偼撦妏乮捈妏偱偼側偄乯 丂丂偟偨偑偭偰丆丂傂偟宍 俋丂摍掙乮掙曈偑摍偟偄乯丆摍崅乮崅偝偑摍偟偄乯 丂側嶰妏宍偼摍愊乮柺愊偑摍偟偄乯偐傜丆僄 10丂佢俙俷俛亖2佢俠亖2亊30亖60亱 丂丂丂佢俙俢俛亖30亄50亖80亱 丂丂傛偭偰丆佢俷俙俢亖80亅60亖20亱 |
| 乵僩僢僾偵栠傞乶 乵慜儁乕僕偵栠傞乶丂乵師儁亅僕偵恑傓乶 |
丂