|
惓丂摎丂俀 | ||||
| 俋丂撊栘摴丂乣丂16丂晉嶳導 | |||||
|
惓丂摎丂俀 | ||||
| 俋丂撊栘摴丂乣丂16丂晉嶳導 | |||||
| 俋撊栘導 | 侾丂亅4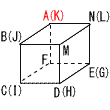 俀丂4倎2倐3 俀丂4倎2倐3俁丂倶2亅6倶亄9 係丂2併6亄併6亖3併6 俆丂佢倶亖105-70亖35亱 俇丂(倶亄3)(倶亅2)亖0傛傝丆 丂丂丂丂倶亖亅3丆2 俈丂塃恾傛傝丆揰俲 俉丂値偼4偲6偺嵟彫岞攞悢偩偐傜丆値亖12 |
13搶嫗搒 |
侾丂9亅18亖亅9 俀丂倎亅8倐亅2倎亄14倐亖亅倎亄6倐 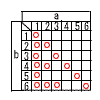 俁丂5亄3併5亅4亖1亄3併5 俁丂5亄3併5亅4亖1亄3併5係丂亅2倶亖亅14傛傝丆倶亖7 俆丂忋幃亊5亅壓幃傛傝丆倶亖2 丂丂偙傟傪忋幃偵戙擖偟偰丆8亄倷亖9 丂丂傛偭偰丆倶亖2倷亖1 俇丂倶亄2亖亇6傛傝丆倶亖亅2亇6 丂丂傛偭偰丆倶亖4丆亅8 俈丂塃恾偺傛偆偵丆慡晹偱14捠傝 俉丂佢俛俷俠亖60亱佢俛俙俢亖15亱 丂丂佢俙俤俷亖60亅15亖45亱 丂丂傛偭偰丆佢俙俤俠亖180亅45亖135亱 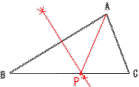 俋丂曈俙俛偺悅捈擇摍暘慄傪堷偒丆曈俛俠偲偺岎揰傪俹偲偡傟偽傛偄丅 俋丂曈俙俛偺悅捈擇摍暘慄傪堷偒丆曈俛俠偲偺岎揰傪俹偲偡傟偽傛偄丅丂 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 10孮攏導 | 侾丂亅42 俀丂4倎
丂丂丂亖亅9倷2 乵俀斣栤戣乶丂乣偍傑偗乣 侾丂愒忛嶳丂379丂丂丂柇媊嶳丂亅345
俁
係丂楢懕偡傞俀偮偺帺慠悢傪倶丆倶亄1偲偡傞偲丆 丂丂丂倶2亄(倶亄1)2亖145丂偨偩偟丆倶亜0 丂丂丂偙傟傪夝偔偲丆(倶亄9)(倶亅8)亖0傛傝丆 丂丂丂倶亜0偩偐傜丆倶亖8 丂丂丂丂丂傛偭偰丆8偲9 |
14恄撧愳導 | 侾丂亅5亅8亖亅13 俀丂2亄12亖14
俈丂倶2亄4倶亄4亅倶2亄倶亄12亖5倶亄16 乵俀斣栤戣堦晹乶丂乣偍傑偗乣 侾丂倶2亅5倶亄4亅10亖倶2亅5倶亅6 丂丂丂亖(倶亅6)(倶亄1) 俀丂倶亄5亖亇併7傛傝丆倶亖亅5亇併7 俁丂忋幃亊5亄壓幃亊3傛傝丆倶亖2 丂丂偙傟傪忋幃偵戙擖偟偰丆4亄3倷亖1 丂丂傛偭偰丆倶亖2丆倷亖亅1 係丂倶亖2偺偲偒丆倷亖亅2 丂丂倶亖4偺偲偒丆倷亖亅8
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 11嶉嬍導 | 乵慜婜乶 侾丂3倎丂丂丂俀丂亅6亄4亖亅2 俁丂2併2亅5併2亖亅3併2 係丂梌幃亖(倶亅7)(倶亄3)亖(17亅7)(17亄3)亖200 俆丂倶亅4亖亇併3傛傝丆倶亖4亇併3 俇丂忋幃亄壓幃亊2傛傝丆7倶亖14偱丆倶亖2 丂丂偙傟傪忋幃偵戙擖偟偰丆2亄2倷亖4 丂丂丂丂傛偭偰丆倶亖2丆倷亖1 俈丂僀 俉丂掙柺偺敿宎傪倰偲偡傞偲丆 丂丂丂丂2兾倰亖12兾亐2亖6兾傛傝丆倰亖3 丂丂傛偭偰丆32兾亖9兾cm2 俋丂(A丆B丆C)亖(3,1,1)丂(2,1,2)丂(2,2,1) 丂丂丂丂 (1,3,1)丂(1,2,2)丂(1,1,3) 偺丂俇捠傝 乵屻婜乶 侾丂亅6倶丂丂丂俀丂亅4亄6亖2 俁丂2併7亄3併7亖5併7 係丂梌幃亖(倶亅3)2亖(併3亄3亅3)2 丂丂丂丂亖(併3)2亖3 俆丂倶亄3亖亇併11傛傝丆倶亖亅3亇併11 俇丂忋幃亄壓幃亊3傛傝丆32倶亖32偱 丂丂丂丂倶亖1 丂丂偙傟傪壓幃偵戙擖偟偰丆10亄倷亖9 丂丂丂丂傛偭偰丆倶亖1丆倷亖亅1 俈丂倷亖倎倶2偵倶亖2丆倷亖12傪戙擖偡傞偲丆 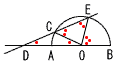 丂丂丂丂12亖4倎傛傝丆倎亖3 丂丂丂丂12亖4倎傛傝丆倎亖3丂丂傛偭偰丆倷亖3倶2 俉丂5亊4亐2亖10捠傝 俋丂佢俙俷俠亖倶偲偡傞偲丆 丂丂丂丂俷俠亖俠俢傛傝丆佢俠俢俷亖倶 丂丂傛偭偰丆佢俷俠俤亖佢俷俤俠亖2倶 丂丂偟偨偑偭偰丆佢俛俷俠亖3倶偲側傞偐傜丆 丂丂丂丂屖俙俠丗屖俛俤亖侾丗3丂丂丂丂丂丂丂丂 |
15怴妰導 | 侾丂7/12 俀丂亅4 俁丂6倎亄3倐亅倎亄4倐亖5倎亄7倐 係丂3倶亖9傛傝丆倶亖3 俆丂倎4倐7 俇丂忋幃亊2亄壓幃傛傝丆倶亖4 丂丂偙傟傪壓幃偵戙擖偟偰丆4亄2倷亖2 丂丂傛偭偰丆倶亖4丆倷亅亅1 俈丂3併2亅併2亖2併2 俉丂(倶亅3)(倶亅9)亖0傛傝丆倶亖3丆9 俋丂乮2丆亅1)傪捠傞偐傜丆嵗昗傪戙擖偟偰丆 丂丂倎亖2亊(亅1)亖亅2
丂丂丂丂4亖倎亄6傛傝丆倎亖亅2 丂丂倷亖亅2倶亄6偵丆(倫丆0)傪戙擖偟偰丆 丂丂丂丂0亖亅2倫亄6傛傝丆倫亖3 11丂佢俠俙俛亖佢俷俠俙亖25亱(嶖妏) 丂丂丂傛偭偰丆佢倶亖佢俠俙俛亊2亖50亱 12丂倶丗6亖6丗9傛傝丆9倶亖36 丂丂丂傛偭偰丆倶亖4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 12愮梩導 | 侾丂-5亅5亖亅10 俀丂12亄3亖15 俁丂倶亅8倷亅4倶亄28倷亖亅3倶亄20倷 係丂2倷亖10倶亄1
俇丂倶2亅4倶亅12亄16亖倶2亅4倶亄4 丂丂丂丂亖(倶亅2)2 丂 |
16晉嶳導 | 侾丂8亅3亖5丂丂丂俀丂亅1/15 俁丂10倎亅5亅7倎亄9亖3倎亄4 係丂3倶倷亅1 俆丂2併5亅併5亖併5 俇丂(倶亅8)(倶亄1)亖0傛傝丆倶亖8丆亅1 俈丂倷亖倎倶偵(3丆亅9)傪戙擖偟偰丆亅9亖3倎 丂丂丂丂傛偭偰丆倎亖亅3 丂丂倷亖亅俁倶偵倶亖亅2傪戙擖偡傞偲丆 丂丂丂丂倷亖(亅3)亊(亅2)亖6 俉丂倶亖亅2偺偲偒丆倷亖5 丂丂倶亖6偺偲偒丆倷亖亅3 丂丂傛偭偰丆亅3亝倷亝5 俋丂佢俙亖90亅40亖50亱 丂丂佢俙俛俢亖180亅50亅60亖70亱 丂丂傛偭偰丆佢倶亖佢俙俛俢亖70亱 10丂嘆曈俛俠偺拞揰俵傪偲傞 丂丂 嘇俠俵偺挿偝偩偗丆斀懳懁偵俠俹傪偲傞 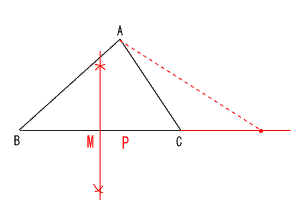 |
| 乵僩僢僾偵栠傞乶 乵慜儁乕僕偵栠傞乶丂乵師儁亅僕偵恑傓乶 |
丂