全国公立高校入試 　１番問題　【平成２２年春】

（３１）　鳥取県

学習日　 　　 　　月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１	(1)　−2−(−10) 　　　　　　　　　　　　　　　　　　　　　　　　　 .	５	ｙはｘ の一次関数で，そのグラフが点(1，3)を通り，傾き2の直線であるとき，この一次関数の式を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.
	(2)　 １ − １ ３ ２ 　　　　　　　　　　　　　　　　　　　　　　　　　 . .	６	関数　ｙ＝ａｘ2　について，ｘ の値が1から3まで増加するときの変化の割合が12であるとき，ａの値を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
	(3)　√8− 　2 . √2 　　　　　　　　　　　　　　　　　　　　　　　　　 .	７	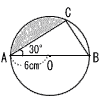右の図ABを直径とする半径6cmの円周上に，∠BAC=30°となる点Cがある。 　このとき，図の色のついた部分の面積を求めなさい。 　ただし，円周率はπとする。 　　　　　　　　　　　　　　　　　　　　　.
	(4)　4(ａ−1)−(ａ＋3) 　　　　　　　　　　　　　　　　　　　　　　　　　.	８	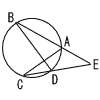右の図のように，同一円周上に４点A，B，C，Dがあり，A，Bを通る直線と，C，Dを通る直線が，点Eで交わっている。 　このとき，△BDE∽△CAEであることを証明しなさい。 ［証明］
２	ａｂ＋2ｂ　を因数分解しなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
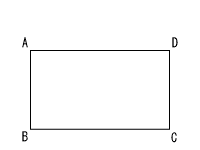
３	二次方程式　ｘ2−7ｘ＋10＝0　を解きなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	９	右の図の長方形ABCDの辺AD上に，∠CBE=60°となる点Eを，コンパスと定規を用いて作図しなさい。 　なお，作図に用いた線は，消さずに残しておきなさい。
４	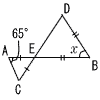右の図のように，線分ＡＢとＣＤが， 　　ＡＥ＝ＣＥ，ＥＢ＝ＤＢ となるように，点Ｅで交わっている。 　このとき，∠ｘ の大きさを求めなさい。 　　　　　　　　　　　　　　　　　　　　 .