|
(25) 滋賀県 | 学習日 月 日( ) |
|
(25) 滋賀県 | 学習日 月 日( ) |
| 1 | . |
4 | 学さんは,直線 【学さんの考えた方法】 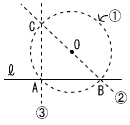 ① 直線 ① 直線② 円Oと直線 ③ 直線BOと円Oとの交点のうち,Bと異なる点をCとし,直線ACをひく。 |
|||
. . |
||||||
| (3) 3y2÷xy×(2x)2 . |
学さんが考えた方法で作図した直線ACが,直線 |
|||||
| (4) (x+5)(x-5)+2x . |
||||||
. |
5 | 図2のように,1列に並んだマス目の1つにコマを置き,さいころを投げて,出た目が偶数ならその目の数だけ右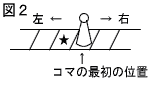 へ,奇数ならその目の数だけ左へコマを動かすこととする。 いま,1回さいころを投げてコマを動かし,さらにもう1回さいころを投げてそのコマを動かす。 このようにして2回動かした後,コマが止まる位置について,次の①,②の問いに答えなさい。 へ,奇数ならその目の数だけ左へコマを動かすこととする。 いま,1回さいころを投げてコマを動かし,さらにもう1回さいころを投げてそのコマを動かす。 このようにして2回動かした後,コマが止まる位置について,次の①,②の問いに答えなさい。① コマが最初の位置の左どなり(図2の★の位置)のマス目に止まるようなさいころの目の出方は,何通りあるか。 求めなさい。 . ② コマが最初の位置より右側のマス目に止まる確率を求めなさい。 ただし,さいころの1から6までのどの目が出ることも同様に確からしいものとする。 . |
||||
| 2 | ある数xの2乗とxの和が2になった。 このxを求めなさい。 . |
|||||
| 3 | 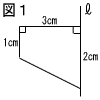 図1のような四角形を,直線 図1のような四角形を,直線. |
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |