|
(24) 三重県 | 学習日 月 日( ) |
|
(24) 三重県 | 学習日 月 日( ) |
| 前 期 | 後 期 | |||||||||
| 1 | . |
1 | . |
|||||||
| 2 | 3(4x+y)−5(3x−y) . |
2 |
|
|||||||
| 3 | 等式 2a+3b=7 をaについて解きなさい。 . |
3 | a=−3のとき,3a−(2a−5) の値を求めなさい。 . |
|||||||
| 4 |
|
4 | 6x×2xy3÷(−4y2) . |
|||||||
| 5 | 二次方程式 (x+4)(x−3)=8 を解きなさい。 . |
5 |
. |
|||||||
| 6 | yはxに反比例し,x=3のときy=−8である。 yをxの式で表しなさい。 . |
6 | (3+2√5)(3−2√5) . |
|||||||
| 7 | 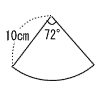 右の図のような,半径10cm,中心角72°のおうぎ形がある。 このおうぎ形の面積を求めなさい。 右の図のような,半径10cm,中心角72°のおうぎ形がある。 このおうぎ形の面積を求めなさい。ただし,円周率はπとする。 . |
7 | 二次方程式 x2+8x−1=2x−6 を解きなさい。 . |
|||||||
| 8 | 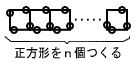 右の図のように,マッチ棒を並べて正方形をn個つくるとき,必要なマッチ棒の本数をnを使って表しなさい。 右の図のように,マッチ棒を並べて正方形をn個つくるとき,必要なマッチ棒の本数をnを使って表しなさい。. |
 |
||||||||
| 9 | 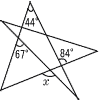 右の図で,∠xの大きさを求めなさい。 右の図で,∠xの大きさを求めなさい。. |
|||||||||
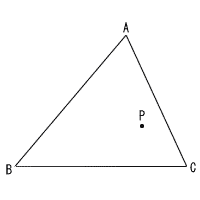
| 10 | 右の図のような三角形の紙があり,3つの頂点をそれぞれA,B,Cとする。 この紙を点Pを通る直線を折り目として,頂点Aが辺BC上にくるように折り曲げる。 折り目とした直線と辺AB,辺ACとの交点をそれぞれQ,Rとするとき,交点Q,Rを定規とコンパスを用いて作図しなさい。 なお,作図に用いた線は消さずに残しておきなさい。 |
|||||||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |