全国公立高校入試 　１番問題　【平成２２年春】

（１１）　埼玉県

学習日　 　　 　　月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

前　　　　　期		後　　　　　期
１	5ａ−2ａ 　　　　　　　　　　　　　　　　　　　　　　　　　 .	１	3ｘ×(−2) 　　　　　　　　　　　　　　　　　　　　　　　　　 .
２	(−2)×3＋4 　　　　　　　　　　　　　　　　　　　　　　　　　 .	２	(−8)÷2＋6 　　　　　　　　　　　　　　　　　　　　　　　　　 .
３	√8−5√2 　　　　　　　　　　　　　　　　　　　　　　　　　 .	３	√28＋3√7 　　　　　　　　　　　　　　　　　　　　　　　　　.
４	ｘ＝17のとき，ｘ2−4ｘ−21　の値を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.	４	ｘ＝√3＋3のとき，ｘ2−6ｘ＋9　の値を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.
５	２次方程式　(ｘ−4)2＝3　を解きなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	５	２次方程式　(ｘ＋3)2＝11　を解きなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.
６	連立方程式　｛　 ｘ＋2ｙ＝4 　を解きなさい。 3ｘ−ｙ＝5 　　　　　　　　　　　　　　　　　　　　　　　　　 .	６	連立方程式　｛　 2ｘ−3ｙ＝5 　を解きなさい。 10ｘ＋ｙ＝9 　　　　　　　　　　　　　　　　　　　　　　　　　.
７	ｘ軸を対称の軸として，関数 ｙ＝2ｘ2のグラフと線対称であるのはどの関数のグラフですか。次のア〜オの中から正しいものを１つ選び，その記号を書きなさい。 ア　ｙ＝2ｘ2　 　イ　ｙ＝−2ｘ2　 　ウ　ｙ＝−ｘ2 エ　ｙ＝ １ ｘ2　 　オ　ｙ＝− １ ｘ2 ２ ２ 　　　　　　　　　　　　　　　　　　　　　　　　　 .	７	ｙはｘの２乗に比例し，ｘ＝2のときｙ＝12です。　このとき，ｙをｘの式で表しなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　.
８	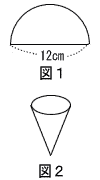右の図１のような，直径12cmの半円の形の紙があります。　この紙を，重ならないように折り曲げて図２のような底面のない円すいをつくります。　別の紙で，この円すいの底面をつくります。　この底面の面積を求めなさい。 　ただし，円周率はπとします。 　　　　　　　　　　　　　　　　　　　　　 .	８	Ａ，Ｂ，Ｃ，Ｄ，Ｅの５人の生徒の中から２人の委員を選ぶとき，その選び方は全部で何通りあるか求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
９	５本の新しいえんぴつすべてを，Aさん，Bさん，Cさんの３人に分けることにします。　分け方は全部で何通りあるか求めなさい。　ただし，えんぴつはすべて同じものとし，３人全員が少なくとも１本は受け取るものとします。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	９	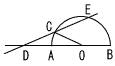線分ＡＢを直径とする半円Ｏがあります。　右の図のように，弧ＡＢ上の点Ｃと，線分ＡＢをＡの方へ延長した線上の点Ｄを，∠ＯＣＤが鈍角で，ＯＣ＝ＣＤとなるようにとります。　２点Ｃ，Ｄを通る直線と弧ＡＢとの交点をＥとするとき，弧ＡＣと弧ＢＥの長さの比を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
（　10〜11　省　略　）		（　10〜11　省　略　）