|
(5) 山形県 | 学習日 月 日( ) |
|
(5) 山形県 | 学習日 月 日( ) |
| 1 | .
. (3) 3(2x+y)-5(x-3y) . (4) (√2+1)2-√32 . |
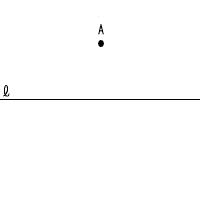
4 | ただし,作図に使った線は残しておくこと。 【条件】 ひし形ABCDは,直線 【手順】 はじめに,点Cを作図し,次に,直線 |
|||||||||||
 |
||||||||||||||
| <選択問題> 下の(A),(B)のどちらか1問を選び,答えなさい。 | ||||||||||||||
| 2 | 2次方程式 (x+3)(x-3)=-2x-1 を解きなさい。 解き方も書くこと。 . |
5 |
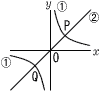 (A) 右の図において,①は反比例 y=a/x のグラフ,②は比例 y=x のグラフであり,①と②は2点P,Qで交わっている。 線分PQの長さが6√2であるとき,aの値を求めなさい。 (A) 右の図において,①は反比例 y=a/x のグラフ,②は比例 y=x のグラフであり,①と②は2点P,Qで交わっている。 線分PQの長さが6√2であるとき,aの値を求めなさい。. |
|||||||||||
| 3 | 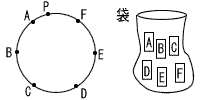 のカードが示す円周上の2点と点Pの3点を頂点とする三角形をつくるとき,その三角形が直角三角形になる確率を求めなさい。 のカードが示す円周上の2点と点Pの3点を頂点とする三角形をつくるとき,その三角形が直角三角形になる確率を求めなさい。ただし,どのカードが取り出されることも同様に確からしいものとする。 . |
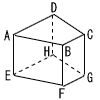 (B) 右の図のように,AD//BCの台形ABCDを底面とする四角柱ABCD-EFGHがあり,AB=5cm,BC=2cm,CD=3cm,DA=6cm,AE=4cmである。 (B) 右の図のように,AD//BCの台形ABCDを底面とする四角柱ABCD-EFGHがあり,AB=5cm,BC=2cm,CD=3cm,DA=6cm,AE=4cmである。この四角柱の辺のうち,辺ABとねじれの位置にあるすべての辺の長さを合わせると何cmになるか,求めなさい。 . |
||||||||||||
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |