|
(3) 秋田県 | 学習日 月 日( ) | ||||
|
(3) 秋田県 | 学習日 月 日( ) | ||||
| 次の1〜15の中から,指示された8問について答えなさい。(選択問題) | |||||||
| 1 | 次の3つの数を,数直線上で1からの距離が小さい順に,左から並べて書きなさい。
. |
9 | 同じ値段のノートを10冊買うには,持っているお金では200円足りないが,8冊買うと100円余る。ノート1冊の値段を x 円として,方程式をつくりなさい。ただし,つくった方程式を解く必要はありません。 . |
||||
| 2 | 次の(1),(2)の問いに答えなさい。 (1) 図1のように,長さ2mのテープを3等分したとき,アにあてはまる数を書きなさい。 . 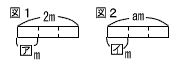 (2) 図2のように,長さamのテープを3等分したとき,イにあてはまる式を書きなさい。 (2) 図2のように,長さamのテープを3等分したとき,イにあてはまる式を書きなさい。. |
10 | . |
||||
| 11 | 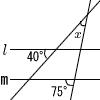 右の図において,2直線 右の図において,2直線. |
||||||
| 3 | 4a2b3÷2ab×(−a2) を計算しなさい。 . |
12 | 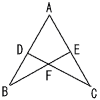 右の図において,線分AB上に点D,線分AC上に点Eがあり,線分CDと線分BEの交点をFとする。AD=AE,∠ADC=∠AEBであるとき,△ACDと合同な三角形を答えなさい。また,それらが合同であることを証明するときに使う三角形の合同条件を書きなさい。 右の図において,線分AB上に点D,線分AC上に点Eがあり,線分CDと線分BEの交点をFとする。AD=AE,∠ADC=∠AEBであるとき,△ACDと合同な三角形を答えなさい。また,それらが合同であることを証明するときに使う三角形の合同条件を書きなさい。. |
||||
| 4 |
. |
||||||
| 5 | 2a+bという式で表されるものを,次のア〜エから1つ選んで記号を書きなさい。
. |
13 | 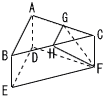 . |
||||
| 6 | x=9.6, y=0.4 のとき,x2+xy の値を求めなさい。 . |
14 | 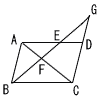 . |
||||
| 7 | √6(√2+√3)−2√3 を計算しなさい。 . |
||||||
| 8 | 方程式 x(x+4)=2x+3 を解きなさい。 . |
15 | 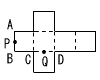 . |
||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |