|
惓丂摎丂侾丂 | |||
| 侾丂杒奀摴丂乣丂俉丂堬忛導 |
|
惓丂摎丂侾丂 | |||
| 侾丂杒奀摴丂乣丂俉丂堬忛導 |
| 侾杒奀摴 | 侾丂(1)丂亅28 丂丂(2)丂9亅40亖亅31 丂丂(3)丂併6亄併6亖2併6 俀丂10偺栺悢偼丂1丆2丆5丆10偺係屄偁傞偐傜丆 丂丂丂4/10亖2/5 俁丂俙(8丆0)丂俛(0丆8)丂偲側傞偐傜丆 丂仮俷俙俛亖1/2亊8亊8亖32乮扨埵偼晄梫乯 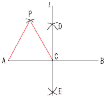 係丂 係丂嘆俙偲俛偐傜僐儞僷僗偱摨偠敿宎偺屖傪偲偭偰丆岎揰俢偲俤傪寢傇 嘇慄暘俙俛偺悅捈擇摍暘慄傪堷偒丆拞揰俠傪偲傞丅 嘊俙偲俠偐傜僐儞僷僗偱俙俠偺挿偝偺敿宎偱屖傪偲偭偰丆岎揰傪俹偲偡傞丅 嘋俹丆俙丆俠傪寢傫偱惓嶰妏宍傪偮偔傞 |
俆嶳宍導 | 侾丂2亅7亄8亖3
係丂5亅3併5亄2併5亖5亅併5 丂乣丂俀斣栤戣偺堦晹丂乮偍傑偗乯丂乣 丂倶2亅6倶亄9亄倶亅15亖0 丂倶2亅5倶亅6亖0 丂(倶亅6)(倶亄1)亖0 丂丂倶亖6丆亅1 |
||||||||||||||||||||||||
| 俀惵怷導 | 侾丂傾丂俈丂丂僀丂亅3丂丂僂丂5亅9亊2亖亅13 丂丂僄丂4倶2倷丂丂僆丂5亄8併5亄1亖21亄8併5 俀丂2亊3亊72 俁丂7倶亅11倶亖14亄2 丂丂亅4倶亖16丂傛傝丆倶亖亅4
丂丂倷亖14/倶偵丆倶亖0.5傪戙擖偟偰丆 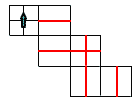 丂丂倷亖28 丂丂倷亖28俇丂佢倶亖90亅58亖32亱 俈丂塃恾 俉丂佢俛俙俤亖佢俠俙俤 丂丂丂亖77亅41亖36亱 丂佢俙俠俛亖180亅36亅77亖67亱丂 |
俇媨忛導 | 侾丂亅3亄8亖5 俀丂4倎亄2亄3倎亅3亖7倎亅1 俁丂(倶亄2)(倶亄4) 係丂3併3亄2併3亅併3亖4併3 俆丂90亄(45亅30)亄倶亖180 丂丂倶亖180亅105亖75亱 |
||||||||||||||||||||||||
| 俁廐揷導 | 侾丂1亅(亅2)亖3丆丂1亅0亖1丆丂3亅1亖2 丂丂傛偭偰丆丂0丆3丆亅2
係丂戙擖朄偱夝偄偰丆倶亖2丆倷亖亅4 俆丂傾丂2倎亄2倐丂丂僀丂併(倎2亄倐2)丂丂僂丂2倎亄倐 丂丂僄丂倎2倐丂丂丂傛偭偰丆丂僂 俇丂梌幃亖倶(倶亄倷)亖9.6亊(9.6亄0.4)亖96 俈丂併12亄併18亅2併3亖3併2 俉丂倶2亄4倶亖2倶亄3 丂丂倶2亄2倶亅3亖0 丂丂(倶亄3)(倶亅1)亖0丂傛傝丆倶亖亅3丆1 俋丂10倶亅200亖8倶亄100 10丂乷併(2倶)亄併(3倷)乸2亖2倶亄3倷亄2併6併倶倷 丂丂併倶倷亖併6丆2併6(併24)丆3併6(併54) 丂丂丂丂偱偁傟偽傛偄偐傜丆 丂丂倶倷亖6偲側傞侾偗偨偺帺慠悢夝偼丆 丂丂丂(倶丆倷)亖(1丆6)丂(2丆3)丂(3丆2)丂(6丆1) 丂丂倶倷亖24偲側傞侾偗偨偺帺慠悢夝偼丆 丂丂丂(倶丆倷)亖(3丆8)丂(4丆6)丂(6丆4)丂(8丆3) 丂丂倶倷亖54偲側傞侾偗偨偺帺慠悢夝偼丆 丂丂丂(倶丆倷)亖(6丆9)丂(9丆6)偱丆丂寁丂10慻 11丂倶亄40亖75丂傛傝丆35亱 12丂侾曈偲偦偺椉抂偺妏偑偦傟偧傟摍偟偄 13丂1/3亊(1/2亊2亊3)亊3亖3 丂丂1/2亊4亊6亊3亅3亖33cm3 14丂EF=4亊(2/3)亖8/3 丂丂倶丗(倶亄8/3亄4)亖1丗3丂傛傝丆倶亖10/3cm 15丂62亄(3併2)2亖36亄18亖54 丂丂傛偭偰丆併54亖3併6cm |
俈暉搰導丂 | 侾丂(1)丂4亄5亖9
丂丂(3)丂亅2併2亄3併2亖併2 丂丂(4)丂亅3倎2倐 俀 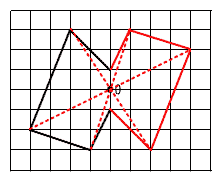 |
||||||||||||||||||||||||
| 係娾庤導 | 侾丂亅5 俀丂亅12/10亖亅6/5 俁丂3亄3併3亄2亖5亄3併3 係丂倶亖4丆亅2 俆丂(倶亄1)(倶亄6)亖0丂傛傝丆倶亖亅1丆亅6 俇丂3倐亖12亅倎
|
俉堬忛導 | 侾丂亅7 俀丂12亅3亖9
|
| 乵僩僢僾偵栠傞乶 丂丂丂丂丂丂丂丂丂乵師儁亅僕偵恑傓乶 |
丂