|
惓丂摎丂係丂 | |||
| 25丂帬夑導丂乣丂32丂搰崻導 |
|
惓丂摎丂係丂 | |||
| 25丂帬夑導丂乣丂32丂搰崻導 |
| 25帬夑導 | 侾丂(1)丂2亅4亖亅2丂丂(2)丂倎亅12
丂丂丂(亅5)2亄(亅5)亄倎亖0 丂丂丂25亅5亄倎亖0傛傝丆倎亖亅20 丂丂傛偭偰尦偺幃偼丆倶2亄倶亅20亖0 丂丂丂(倶亄5)(倶亅4)亖0傛傝丆 丂丂丂懠偺夝偼丆倶亖4 俁丂惓曽宍偺侾曈偼6偩偐傜丆俻(3丆3) 丂丂偙傟傪倷亖倎/倶偵戙擖偡傞偲丆 丂丂丂3亖倎/3傛傝丆倎亖9 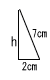 係丂墌偡偄偺崅偝倛傪媮傔傞偲丆 係丂墌偡偄偺崅偝倛傪媮傔傞偲丆丂丂丂倛2亖72亅22亖45傛傝丆 丂丂丂倛亖併45亖3併5 丂丂懱愊亖1/3亊22兾亊3併5亖4併5兾cm3 俆丂崟偺侾曈偑値屄偲偡傞偲丆 丂丂丂崟偺岄愇偼丆(3値亅3)屄 丂丂丂敀偺岄愇偼丆(3値亅3亄36)屄 丂丂傛偭偰丆(3値亅3)亄(3値亅3亄俁俇)亖120 丂丂丂6値亄.30亖120偱丆値亖15屄 丂丂乵暿夝乶 丂丂丂崟偺侾曈偑値屄偲偡傞偲丆 丂丂丂1亄2亄丒丒丒亄値亖120 丂丂丂値(値亄1)/2亖120傛傝丆 丂丂丂値2亄値亅240亖0偱丆 丂丂丂丂(値-15)(値亄16)亖0 丂丂丂丂値亜0傛傝丆値亖15屄 俇丂(1)丂嶌恾曽朄偼丆 丂丂丂嘆拞怱O偐傜抧柺偵悅慄傪偍傠偡 丂丂丂嘇悅慄偲墌O偺岎揰P傪偲傞 丂丂丂嘊P偐傜墌廃忋偵丆敿宎偺挿偝偺揰Q傪偲傞 丂丂丂嘋O偐傜墌廃忋偵丆敿宎偺挿偝偺揰E傪偲傞 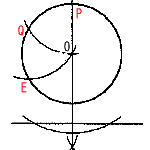 丂丂(2)丂斣崋俈偐斣崋侾侾偵忔傟偽傛偄丅 丂丂丂丂丂丂斣崋俈偵側傞偺偼丆1+6丆2+5丆3+4 丂丂丂丂丂丂丂丂4+3丆5+2丆6+1偺俇捠傝 丂丂丂丂丂斣崋侾侾偵側傞偺偼丆 丂丂丂丂丂丂丂丂5+6丆6+5偺俀捠傝 丂丂丂丂丂傛偭偰丆妋棪亖(6亄2)/36亖2/9丂丂丂丂丂丂丂丂丂 |
29撧椙導 | 侾丂(1)丂亅36 丂丂(2)丂3倶亄6倷亄2倶亅2倷亖5倶亄4倷
丂丂(4)丂2亄2併2亅3亄1亖2併2 俀丂忋幃亅壓幃傛傝丆 丂丂丂4倷亖亅4偱丆倷亖亅1 丂丂偙傟傪忋幃偵戙擖偡傞偲丆 丂丂丂倶亄3亊(亅1)亖2傛傝丆倶亖5 丂丂傛偭偰丆倶亖5丆倷亖亅1 俁丂倶亖5傪戙擖偡傞偲丆 丂丂丂5倎亄3亖8亊5亅7 丂丂丂5倎亖30偱丆倎亖6 係丂掙柺偺敿宎傪倰偲偡傞偲丆
俆丂榓偑嬼悢偲側傞偺偼丆 丂1+3丆1+5丆2+4丆2+6丆3+1丆3+5丆4+2丆4+6丆 丂5+1丆5+3丆6+2丆6+4丂偺12捠傝 丂丂傑偨丆俀枃偺僇乕僪偺弌曽偼丆 丂丂丂6亊5亖30捠傝
|
||||||||||||||||||||||
| 26嫗搒晎 | 侾丂16亅1亖15 俀丂6倎亅5倐亅2倎亅6倐亖4倎亅11倐 俁丂併2亅3併2亄5併2亖3併2 係丂3(倶亅3)(倶亄1)亖0傛傝丆倶亖3丆亅1 俆丂愗曅(0,1)傪捠傝丆孹偒亅2/3(塃傊俁恑傫偱丆壓傊俀偝偑傞)偺捈慄 俇丂忋幃亊4傛傝丆8倶亄12倷亖亅20丂丒丒丒傾 丂丂壓幃亊3傛傝丆9倶亅12倷亖丂54丂丒丒丒僀 丂傾亄僀傛傝丆17倶亖34偲側偭偰丆倶亖2 丂偙傟傪忋幃偵戙擖偟偰丆2亊2亄3倷亖亅5 丂丂傛偭偰丆3倷亖亅9偱丆倷亖亅3 丂丂丂丂倶亖2丆倷亖亅3 俈丂倶亖亅4偺偲偒丆倷亖1/2亊16亖8 丂丂倶亖亅2偺偲偒丆倷亖1/2亊4亖2
|
30榓壧嶳導 | 侾丂(1)丂亅5丂丂(2)丂1亅2/3亖1/3 丂丂(3)丂6倶亅7倷亅4倶亅倷亖2倶亅8倷 丂丂(4)丂3併5亅2併5亖併5 丂丂(5)丂1亅倎2亄2倎2亖1亄倎2 俀丂(倶亅8)(倶亄1)亖0傛傝丆倶亖8丆亅1 俁丂佢倶亖(180亅130)亄60亖110亱
丂丂 |
||||||||||||||||||||||
| 27戝嶃晎 | 丂丂乵A慖戰乶 侾丂亅俈 俀丂8倎亄3倐 俁丂併5 係丂倶俀亅9倷俀 俆丂(倶亅7)(倶亄4) 俇丂2/5 俈丂嘆丂僀丂丂嘇丂僂 |
31捁庢導丂 | 侾丂(1)丂9亅7亖2
丂丂(4)丂6倶亅8亅倶亅2亖5倶亅10 俀丂忋幃亄壓幃亊4傛傝丆 丂丂丂11倶亖33偱丆倶亖3 丂丂偙傟傪壓幃偵戙擖偡傞偲丆 丂丂丂2亊3亅倷亖8偱丆倷亖亅2 丂丂傛偭偰丆倶亖3丆倷亖亅2 俁丂倷亖倠倶偵(2丆亅6)傪戙擖偡傞偲丆 丂丂丂亅6亖2倠偱丆倠亖亅3 丂丂傛偭偰丆幃偼倷亖亅3倶 丂丂倶亖亅2偺偲偒丆倷亖6 丂丂倶亖1偺偲偒丆倷亖亅3 丂丂傛偭偰丆亅3亝倷亝6 丂丂丂倎亖亅3丆倐亖6 係丂(倎丆倐)亖(1,1)丒丒丒(1,6) (2,2) (2,4) (2,6) 丂丂丂丂丂丂丂(3,3) (3,6) (4,4) (5,5) (6,6) 丂丂丂偺14捠傝偩偐傜丆14/36亖7/18 俆丂柺愊亖1/2(2亄4)(4倎亅倎)亖9倎亖6 丂丂丂傛偭偰丆倎亖6/9亖2/3 俇丂佢俠俷俛亖28亊2亖56亱 丂丂佢俙俛俷亖佢俠俙俛亖28亱(嶖妏) 丂丂傛偭偰丆佢倶亖180亅56亅28亖96亱 俈丂廳側傞偺偼惓曽宍偺柺愊偺1/4偩偐傜丆 丂丂丂2倎2亅1/4倎2亖7/4倎2亖112 丂丂傛偭偰丆倎2亖64傛傝丆倎亖8 俉丂仮俙俛俫偲仮俙俠俫偵偍偄偰丆 丂丂丂丂佢俙俫俛亖佢俙俫俠亖90亱乮壖掕乯 丂丂丂丂俙俛亖俙俠丂乮壖掕乯 丂丂丂丂俙俫亖俙俫丂乮嫟捠乯 丂丂捈妏嶰妏宍偺幬曈偲懠偺侾曈偑摍偟偄偐傜丆 丂丂丂丂仮俙俛俫佭仮俙俠俫 丂丂傛偭偰丆俛俫亖俠俫 俋丂(1)丂俛俠偺悅捈擇摍暘慄傪堷偔丅 丂丂(2)丂俠偐傜悅慄傪壓傠偡丅 丂丂(3)丂俠偲慄懳徧偽揰俠乫傪偲傞丅 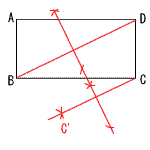 |
||||||||||||||||||||||
| 丂丂乵B慖戰乶 侾丂亅俇
俁丂49 係丂22 俆丂5/12 俇丂俙(倎丆倎俀)偲偡傞偲丆 丂丂丂俛(倎亅1丆(倎亅1)俀)丆俠(倎亄1丆(倎亄1)俀) 丂丂丂偲側傞偐傜丆 丂丂捈慄俛俠偺孹偒傪媮傔傞偲丆
| |||||||||||||||||||||||||
| 28暫屔導 | 侾丂3亄5亖8
係丂4併3亅2併3亖2併3 俆丂俷偲俠傪寢傫偱峫偊傞偲丆 丂佢倶亖佢俛俷俠亄佢俠俷俢亖40亊2亄30亊2亖140亱 俇丂倷亖倎/倶偵丆倶亖3丆倷亖亅4傪戙擖偡傞偲丆 丂亅4亖倎/3傛傝丆倎亖亅12 丂丂傛偭偰丆倷亖亅12/倶 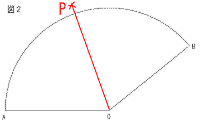 俈丂俙偲俛偐傜丆俙俹亖俛俹偲側傞揰俹傪僐儞僷僗偱嶌恾偟丆俷偲俹傪寢傋偽傛偄丅 俈丂俙偲俛偐傜丆俙俹亖俛俹偲側傞揰俹傪僐儞僷僗偱嶌恾偟丆俷偲俹傪寢傋偽傛偄丅 |
32搰崻導 | 侾丂5亄4亖9 俀丂亅5倶亖亅10傛傝丆倶亖2 俁丂(2倶亄5)(2倶亅5) 係丂梌幃亖(倶亅1)2亖(併2亄1亅1)2亖2 俆丂倶亖亅1偺偲偒丆倷亖(亅1)2亖1 丂丂倶亖2偺偲偒丆倷亖22亖4 丂丂傛偭偰丆0亝倷亝4 俇丂倶亄5亖亇1傛傝丆 丂丂丂倶亖亅5亇1亖亅4丆亅6 俈丂俙俛丆俙俠丆俙俢丆俛俠丆俛俢丆俠俢偺俇捠傝
丂丂仮AEG偱丆FH=1/2GE亖3/2 10丂佢AOB=65亊2亖130亱 丂丂 佢P=360亅130亅90亅90亖50亱 丂 |
| 乵僩僢僾偵栠傞乶 乵慜儁乕僕偵栠傞乶 乵師儁亅僕偵恑傓乶 |