|
正 答 3 | |||
| 17 石川県 〜 24 三重県 |
|
正 答 3 | |||
| 17 石川県 〜 24 三重県 |
| 17石川県 | 1 (1) 4−7−8=−11 (2) 25−24=1
2 (x+6)2=49より,x+6=±7で, x=±7−6=1,−13 3 両辺を2乗して,64<a<67.24より, a=65,66,67 4 男子4人から1人選ぶ方法は4通り 女子3人から1人選ぶ方法は3通り 男女7人から2人選ぶ方法は, 7×6÷2=21通り よって,4×3÷21=12/21=4/7 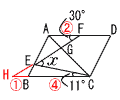 5 ∠x=30+11=41° 5 ∠x=30+11=41°FEを延長してCBの延長線との交点Hをとる。 △AEF∽△BEH(2:1)より, △AGF∽△CGH(2:5) よって,AG:4=2:5で, AG=8/5cm (1.6cm) |
21岐阜県 | 1 4−5=−1 2 8x−2y−7x+5y=x+3y 3 x−5=±2より, x=5±2=7,3
6 点対称は,180回転して重なる図形だから, 5,オは正しくない。 よって,ア,イ,エ 7 (1) 点AからBDと平行な直線 (2) CDを延長し, (3) PとBを結ぶ。 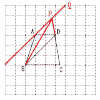 |
||||||||||||||||||||||||||||||||||||
| 18福井県 | 1 (1) 5−14=−9 (2) 2x−3y+8x−4y=10x−7y
2 弧AE+弧EBは半円だから, それに対応する円周角の和は, ∠ACE+∠EDB=180÷2=90° よって,∠x=90−28=62° 3 x2−7x+12=2x2−18 x2+7x−30=0 (x−3)(x+10)=0より,x=3,−10 4 表を作って,グラフに点をとる
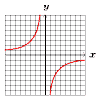 5 CF,FD,FEの3つ |
22静岡県 | 1 (1) 4−21=−17 (2) 2a−3b
(4) 5−2√15+3−4√15=8−6√15 2 両辺×8より,8a=5b+3c 3c=8a−5b
3 x2+2x−24=0 (x+6)(x−4)=0 x=−6,4 |
||||||||||||||||||||||||||||||||||||
| 19山梨県 | 1 −6
4 3√2+2√2=5√2
〜 2番問題 (おまけ) 〜 1 a×3=3a g 2 BC2=22+52=29 よって,BC=√29cm 3 原点Oを通って,傾き−1/2の直線だから,
5 (1) 点Aから,AB=ACとなる点BとCを コンパスでとる。 (2) 点BとCから,BP=CPとなる点Pを コンパスでとる。 (3) PとAを結ぶ。 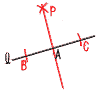 |
23愛知県 | [Aグループ] 1 −2+9=7
5 x2−7x−x+12=0 (x−2)(x−6)=0より,x=2,6 6 ア y=6/xで,○ イ ねじれの位置の場合もあるから× ウ ±6だから× エ 傾き(変化の割合)は一定だから○ したがって,アとエ [Bグループ] 1 11+3−9=5 2 1/2x−2−2/5x+2=1/10x 3 5−4√5+4+10+4√5=19 4 x2−7x−18=0 (x−9)(x+2)=0より,x=9,−2 5 上式×3+下式×4より, 17x=102で,x=6 これを下式に代入して, 12+3y=18で,y=2 よって,x=6,y=2 6 与式=(x+y)(x−y)=(5.7+4.3)(5.7−4.3) =10×1.4=14 |
||||||||||||||||||||||||||||||||||||
| 20長野県 | 1 6−8=−2 2 −45/5=−9 3 −2+16=14 4 √2−3√2=−2√2 5 与式=2a−b=2×1/2−(−5) =1+5=6 6 (3x)2−(7y)2=(3x+7y)(3x−7y) 7 y=a/xに(−2,9)を代入すると, 9=a/−2より,a=−18 8 x=1のとき,y=a x=3のとき,y=9a
9 4枚から2枚取り出す方法は6通り。 このうち,奇数と偶数1枚ずつとなるのは, (1,2) (1,4) (2,3) (3,4) の4通り よって,4/6=2/3 10 1つの外角=360÷8=45° よって,1つの内角は,180−45=135° 11 DE=xとすると, (6−x):x=3:4より,24−4x=3x 7x=24となって,x=24/7(cm) 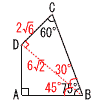 12 CD:6√2=1:√3 12 CD:6√2=1:√3
=1/2×6×6+1/2×2√6×6√2 =18+12√3(cm2) |
24三重県 | A 前期 | ||||||||||||||||||||||||||||||||||||
| 1 −7+2×9=18−7=11 2 与式=2(3x−2y)−3(−x+6y) =6x−4y+3x−18y=9x−22y
4 x=−1を代入すると, (−1)2−a×(−1)+a=13 1+a+a=13より,a=6 元の方程式は,x2−6x+6=13 (x+1)(x−7)=0より, もう1つの解は,x=7 5 a+bが偶数ならば, aもbも偶数である。 × 6 10,12,14,20,24,30,32, 34,40,42 の10通り 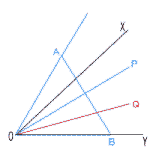 7 イ,ウ 7 イ,ウ8 作図法 (1) 正三角形OABを作図 (2) ∠AOBの二等分線OP を作図 (3) ∠POYの二等分線OQ を作図 |
|||||||||||||||||||||||||||||||||||||||
| B 後期 | |||||||||||||||||||||||||||||||||||||||
3 12a−4b+3a−4b=15a−8b 4 上式×2+下式より, 7x=14で,x=2 これを上式に代入して,4+y=1 よって,x=2,y=−3 5 3√5−2√5+4√5=5√5 6 x2−5x−6=0 (x−6)(x+1)=0より,x=6,−1 |
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] |