全国公立高校入試 　１番問題　【平成２０年春】

（２５）　滋賀県

学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１	(1)　6÷3−4 　　　　　　　　　　　　　　　　　　　　　　　　　 . (2)　3ａ−2(ａ＋6) 　　　　　　　　　　　　　　　　　　　　　　　　　 . (3)　−6ｘ2ｙ÷(−2ｘ)×ｙ 　　　　　　　　　　　　　　　　　　　　　　　　　 . (4)　(2ｘ＋1)2 　　　　　　　　　　　　　　　　　　　　　　　　　 . (5)　 　6 −√27 √3 　　　　　　　　　　　　　　　　　　　　　　　　　 .	５	図３は，１辺に同じ個数の黒の碁石を並べて正三角形の形をつくり，その内側白の碁石を並べた図である。このような方法で，全部で120個の碁石を使って並べたとき，白の碁石が黒の碁石より36個多かった。このとき，正三角形の１辺に並んだ黒の碁石の個数を求めなさい。　　　 　　　　　　　　　　　　　　　　　　　　　　　　　.
		６	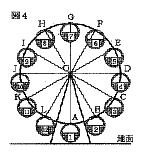図４は，水平な地面に建っている観覧車を，真横から見て図に表したものである。この観覧車には，円Oの周を12等分した点A〜Lに，１〜12の番号が書かれたゴンドラがそれぞれ配置されている。次の(1)，(2)の問いに答えなさい。 (1)　点Aが最も高い位置にきたとき，このときの点Eを，コンパスと定規を使って作図しなさい。ただし，作図に使った線は消さないこと。
２	２次方程式 ｘ2＋ｘ＋ａ＝0 の１つの解が−5のとき，もう１つの解を求めなさい。ただし，ａは定数とする。 . 　　　　　　　　　　　　　　　　　　　　　　　 .
３	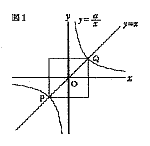図１のように，ｙ＝ｘのグラフとｙ＝ａ/ｘのグラフが２点Ｐ，Ｑで交わっている。線分ＰＱを対角線とする正方形の面積が36のとき，ａの値を求めなさい。 　　　　　　　　　　　　　　　 .
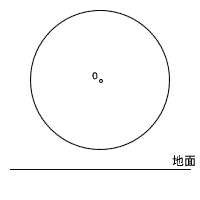
４	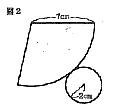図２は，底面の円の半径が2cm，母線の永さが7cmの円すいの展開図である。この円すいの体積を求めなさい。ただし，円周率はπとする。 　　　　　　　　　　　　　　　　.		(2)　３人の人がいて，そのうち２人が番号１と番号６のゴンドラにそれぞれ乗り，あと１人は２つのさいころを同時に投げて，出た目の数の和と同じ番号のゴンドラに乗るとする。３人の乗ったゴンドラが配置されている点を線分で結ぶとき，直角三角形となる確率を求めなさい。ただし，１台のゴンドラには２人まで乗れるものとする。 　　　　　　　　　　　　　　　　.

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい