|
丂乮俆乯丂嶳宍導 | 丂妛廗擔丂 丂丂 寧丂丂 丂丂擔乮丂丂丂丂乯 |
|
丂乮俆乯丂嶳宍導 | 丂妛廗擔丂 丂丂 寧丂丂 丂丂擔乮丂丂丂丂乯 |
乣 報嶞偟偰丄巻偺忋偱傗偭偰僱両 乮暥帤僒僀僘傪彫偵偡傞偲俙係偵廂傑傝傑偡乯乣
| 侾 | (1)丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 .
(3)丂2倎2倐亐6倎倐亊9倐 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 . (4)丂(3併2亅5)(併2亄1) 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 . 丂丂丂 |
係 |  丂偨偩偟丆嶌恾偵巊偭偨慄偼巆偟偰偍偔偙偲丅 亂娭學亃
|
|||||||||||
| 俀 | 丂俀師曽掱幃丂(倶亅2)2亖亅倶亄8丂傪夝偒側偝偄丅夝偒曽傕彂偔偙偲丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 . 丂丂丂 |
俆 | 丂亙慖戰栤戣亜 壓偺(A)丆(B)偺偳偪傜偐侾栤傪慖傃丆摎偊側偝偄丅 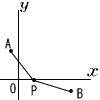 (A)丂 (A)丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 . 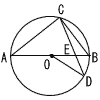 (B)丂塃偺恾偵偍偄偰丆慄暘AB偼揰O傪拞怱偲偡傞墌偺捈宎偱偁傞丅揰C偼偙偺墌偺廃忋偵偁傝丆佢BAC=35亱偱偁傞丅傑偨丆揰C傪傆偔傑側偄屖AB忋偵揰D偑偁傝丆佢BOD=28亱偱偁傞丅慄暘AB偲慄暘CD偲偺岎揰傪E偲偡傞偲偒丆佢BED偺戝偒偝傪媮傔側偝偄丅 (B)丂塃偺恾偵偍偄偰丆慄暘AB偼揰O傪拞怱偲偡傞墌偺捈宎偱偁傞丅揰C偼偙偺墌偺廃忋偵偁傝丆佢BAC=35亱偱偁傞丅傑偨丆揰C傪傆偔傑側偄屖AB忋偵揰D偑偁傝丆佢BOD=28亱偱偁傞丅慄暘AB偲慄暘CD偲偺岎揰傪E偲偡傞偲偒丆佢BED偺戝偒偝傪媮傔側偝偄丅丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 . |
|||||||||||
| 俁 |  丂偨偩偟丆偳偺僇乕僪偑庢傝弌偝傟傞偙偲傕摨條偵妋偐傜偟偄傕偺偲偡傞丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 . 丂丂丂 |
| 乵僩僢僾偵栠傞乶 丂乵慜儁亅僕偵栠傞乶丂乵師儁亅僕偵恑傓乶 乵摎偺儁亅僕偵恑傓乶丂 |