|
正 答 ４ | |||
| 25 滋賀県 〜 32 島根県 |
|
正 答 ４ | |||
| 25 滋賀県 〜 32 島根県 |
| 25滋賀県 | １ (1) ３−４＝−１
(4) ６＋４√６＋４＝１０＋４√６ (5) ３ｂ−２ａ （−２ａ＋３ｂも可） ２ ｘ２−４ｘ−１２＝０ （ｘ−６）（ｘ＋２）＝０より，ｘ＝６，−２ ３ 点Ｐのｙ座標は１２だから， ｙ＝３ｘ２にｙ＝１２を代入して，ｘ＝２ つまり，Ｐ（２，１２）となるから， △ＰＡＯ＝２４×２÷２＝２４ ４ (1) 和が４，８，１２になるのは９通り  よって，９/３６＝１/４(2) （右上図参照） 斜めに２数を組合せると， ６と８で７が２つ，５と９で７が ２つと考えられる  よって，中央の例は７×９＝６３表全体では，７×３６＝２５２ ５ (1) １７÷７＝２（周）・・・３（週目） よって，３×２＋２＝８週 (2) （右図参照） 1班も2班も16週目までに6+1回 残りともに１回当たるには，Ａしかない Ａ |
29奈良県 | １ (１) −２４ (２) ５ｘ＋２ｙ−６ｘ＋２ｙ ＝−ｘ＋４ｙ (３) ａ３ｂ４/ｂ２＝ａ３ｂ２ (４) ３＋２√３−８＋５＝２√３ ２ ２ｘ＝１４より，ｘ＝７ ３ １/３×２２×４＝１６/３ｃｍ２ ４ 選び方は次の６通り ＡとＢ，ＡとＣ，ＡとＤ，ＢとＣ，ＢとＤ，ＣとＤ よって，１/６ ５ ア ｙ＝５ｘ （比例） イ １/２ｘｙ＝１０より，ｙ＝２０/ｘ （反比例） ウ ｙ＝πｘ２ （２乗に比例） エ ｙ＝２（ｘ＋３）より，ｙ＝２ｘ＋６ （１次関数） よって， ウ |
|||||||||
| 26京都府 | １ ６ａ−２−ａ−２＝５ａ−４ ２ (ア) ９/２５ (イ) ９/５＝８１/４５ (ウ) −９/５ (エ) ２５/９＝１２５/４５ よって， ウ，ア，イ，エ ３ （５√３−４√３）×√６÷√２ ＝√３×√６÷√２＝√９＝３ ４ ｘ＋１＝±√７より，ｘ＝−１±√７ ５ ｘ（ｙ２−４）＝ｘ（ｙ＋２）（ｙ−２） |
30和歌山県 | １ (１) −２ (２) ６−２１/４＝３/４ (３) ４√２−５√２＝−√２ (４) −６ａ＋１２ｂ＋５ａ−１０ｂ＝−ａ＋２ｂ (５) （ｘ２＋４ｘ＋４）−（ｘ２＋２ｘ−３） ＝２ｘ＋７ ２ （ｘ＋５）（ｘ−２）＝０より，ｘ＝−５，２ ３ ∠ＣＤＥ＝１２０°より，∠ｘ＝４０° ４ １つの側面は，縦ｂで横ａの長方形 よって，側面積 |
|||||||||
| 27大阪府 | ［Ａ］ １ −３ ２ ３ａ＋８ｂ ３ ５−１＝４ ４ （ｘ−１０）（ｘ＋３） ５ ａ＝ｘｙ＝３×８＝２４より，ｙ＝２４/ｘ これにｘ＝４を代入して，ｙ＝２４/４＝６ ６ 積が奇数になるのは，（奇）×（奇）のとき ３/５×２/４＝６/２０＝３/１０ ７ 傾きは−１/２だから，ｙ＝−１/２ｘ＋２ |
31鳥取県 | １ (1) １０−１４＝−４
(4) ａ２×８ａ＝８ａ３
３ ｘ２−４ｘ＋４＋２ｘ−７＝０ ｘ２−２ｘ−３＝０ （ｘ−３）（ｘ＋１）＝０より，ｘ＝３，−１ ４ (1) （ａ，ｂ）＝(2,6) (6,2) (3,4) (4,3) ４通り 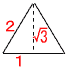 (2) ａ＋ｂ＝３または１２のときだから，（ａ，ｂ）＝(1,2) (2,1) (6,6) の3通りで， ３/３６＝１/１２ ５ （右上図参照） １辺２ｃｍの正三角形の面積は， ２×√３÷２＝√３ だから， 四角すいの底面積は，√３×３＝３√３ｃｍ２ ６ アとエ ７ ＥＣは中心を通るから，∠ＥＢＣ＝９０° 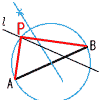 よって，∠Ｃ＝９０−３２＝５８°また，∠ＡＢＥ＝∠ＡＤＥ ＝５８−２５＝３３° ゆえに，∠ＡＢＣ＝33＋90＝123° ８ （右図参照） ＡＢを直径とする円をかく ９ ＡＢ//ＤＦより， △ＡＦＣ＝△ＢＣＦ（面積が等しい） 両辺から△ＣＥＦを引くと，△ＡＥＣ＝△ＢＥＦ |
|||||||||
| ［Ｂ］ １ ７−６−４＝−３
４ １＋３＋５＝９，５＋７＋９＝２１より， 入れ替えて等しくなるのは１と７，３と９だけ ２/（３×３）＝２/９ ５ Ｄ（ｋ，０）とすると，Ｂ（ｋ，３/４ｋ２） 正方形より，２ｋ＝３/４ｋ２ ３ｋ２−８ｋ＝０，３ｋ（ｋ−８/３）＝０ よって，ｋ＝８/３ ｘ＝８/３ |
||||||||||||
| 28兵庫県 | １ −７ ２ （５−６）/１５＝−１/１５ ３ √３−２√３＋３√３＝２√３ ４ −１，０，１ 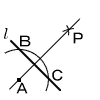 ５ ∠ＡＯＤ＝140°より，∠ｘ＝１４０÷２＝７０° ６ ａ＝ｘｙ＝２×６＝１２だから， ｙ＝12/ｘにｘ＝−3を代入して， ｙ＝−４ ７ (１) Ａを中心に弧をかき，  との交点をＢ，Ｃとする(２) ＢとＣから等距離の点Ｐをとる (３） ＡとＰを結ぶ |
32島根県 | １ ７＋６＝１３ ２ ３√２−４√２＋２√２＝√２ ３ ３ｘ−６ｙ−２ｘ＋６ｙ＝ｘ−２ ４（ｘ＋７）（ｘ−５） ５ １０円硬貨ｘ枚とすると， ５×５ｘ＋１０ｘ＝２１０より，ｘ＝６ ６（枚） ６ ３６０−１１５×２＝１３０（°） ７ １/２×１/２＝１/４ ８ ｙ＝ａｘ２に（３，１８）を代入して，１８＝３２ａ ａ＝２より，ｙ＝２ｘ２ これにｘ＝２を代入すると，ｙ＝２×２２＝８ ９ 切片３より，ｙ＝ａｘ＋３に（２，１）を代入して， １＝２ａ＋３，よってａ＝−１ （ｙ＝）−ｘ＋３ 10 ３２π×２４０/３６０＝６π（ｃｍ３） |
