全国公立高校入試
　１番問題　【平成１８年春】
　（１３）　東京都 　学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１
　− １ ×４＋８
２


　　　　　　　　　　　　　　　　　　　　　　　　　 .
　		 ７ 　右図のように，１，２，３，４，５の数字を１つずつ書いた５枚のカードがある。
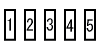　このカードから同時に３枚のカードを取り出すとき，取り出した３枚のカードに書いてある数の和が偶数になる確率を求めよ。
　ただし，どのカードが取り出されることも同様に確からしいものとする。



　　　　　　　　　　　　　　　　　　　　　 .
　　　　
２ 　３(５ａ＋ｂ)−(７ａ−４ｂ)



　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　
３ 　√８−√２×６



　　　　　　　　　　　　　　　　　　　　　　　　　 .
　　　		 ８ 　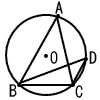右図のように，円Ｏの周上に４点Ａ，Ｂ，Ｃ，Ｄがある。
　点Ａと点Ｂ，点Ａと点Ｃ，点Ｂと点Ｃ，点Ｂと点Ｄ，点Ｃと点Ｄをそれぞれ結ぶ。
　ＡＢ//ＤＣ，∠ＢＤＣ＝４０°，∠ＤＢＣ＝２０°のとき，∠ＢＣＡの大きさは何度か。






　　　　　　 　　　　　　　　　　　 .
　　　
４ 　一次方程式　ｘ−９＝３ｘ＋１　を解け。




　　　　　　　　　 　　　　　　　　　　　　　　　 .
　　　
５
　連立方程式　｛　 ｘ−４ｙ＝６ 　を解け。
３ｘ＋ｙ＝５








　　　　　　　　　　　　　　　　　　　　　　　　 .
　		 ９ 　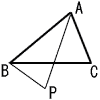右図で，△ＡＢＰは，頂点Ｐが△ＡＢＣの内角である∠ＢＡＣの二等分線上にあり，ＡＢ＝ＡＰの二等辺三角形である。
　右に示した図をもとにして，△ＡＢＰを，定規とコンパスを用いて作図せよ。ただし，作図に用いた線は消さないでおくこと。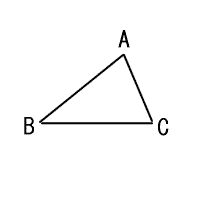
６ 　二次方程式　ｘ２＋ｘ−７２＝０　を解け。








　　　　　　　　　　　　　　　　　　　　　　　　 .
　

　［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい