|
正 答 ５ | |||
| 33 岡山県 〜 40 福岡県 |
|
正 答 ５ | |||
| 33 岡山県 〜 40 福岡県 |
| 33岡山県 | １ −６ ２ ５
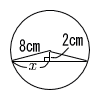 ６ ｘ２−３ｘ−２ｘ−６＝０（ｘ−６）（ｘ＋１）＝０ ｘ＞０だから， ｘ＝６ ７ １２８−４０−６０＝２８° ８ 右図より，ｘ２＋２２＝８２より， ｘ＝√（６４−４）＝√６０＝２√１５ 答 ４√１５（ｃｍ）  ９ 目の出方は，（Ａ，Ｂ）＝（１，４） （４，１） （２，３） （３，２） （４，６） （６，４） ’５，５）の７通りよって，７/３６ （３６分の７） 10 ２乗して比較すると， １６，１８，１５，４９/３（１６．３）だから， 答 √１５，４，７/√３，３√２ 11 (1) 点Ｐから適当な半径の弧をかく (2)  との交点をＡ，Ｂとする(3) Ａ，Ｂから弧をかき，交点Ｐ’をとる ４ ＰとＰ’を結ぶ |
37徳島県 | １ ３０ ２ ４ｘ−２ｘ−６＝２ｘ−６ ３ 両辺×１０より， ５ｘ−１０＝２ｘ−４ ３ｘ＝６より，ｘ＝２ ４ −ｂ＝−２ａ＋５ ｂ＝２ａ−５ ５ ２（ｘ２−６ｘ＋９）＝２（ｘ−３）２ ６ ２乗して比べるとよい
イ ｙ＝２ｘ２（２乗に比例） エ ｙ＝６/ｘ（反比例） したがって，（記号）ウ，（式）ｙ＝−２ｘ ８ （ａ） ∠ＡＢＣ＝１２０÷２＝６０° よって，∠ｘ＝６０−２０＝４０° （ｂ） 素数となるのは，１３，２３，３１，４１，４３の５通り よって，５/（４×３）＝５/１２ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34広島県 | １ ８＋１２＝２０ ２ ６/１４＋７/１４＝１３/１４ ３ −３＋７＝４ ４ ９ｘ＋４ｙ−６ｘ−３ｙ＝３ｘ＋ｙ ５ 上式×３＋下式より，ｘ＝３，ｙ＝−１ ６ √６ ７ ２５ｘ２−ｙ２ ８ （ｘ−４）（ｘ＋２）＝０より，ｘ＝４，−２ |
38愛媛県 | １ −３ ２ ３ａ＋６ｂ−３＋２ａ−６ｂ＝５ａ−３ ３ ２ｘ２−ｘ ４ ５＋４√５＋４−２√５＝９＋２√５ ５ （ｘ２−４）−（ｘ２−ｘ−１２）＝ｘ＋８ 〜 おまけ 〜 （ｘ＋６）（ｘ−５）＝０より，ｘ＝−６，５ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35山口県 | １ ９ ２ −３/１４ ３ ７ａ−２ ４ ２ｘ＋６ ５ （−３）２＋４×２＝１７ 〜 おまけ ［２］ 〜 １ （ｘ＋５）（ｘ＋７）
４ 三平方の定理より，ＡＣ２＋５２＝６２ ＡＣ２＝３６−２５＝１１ よって，ＡＣ＝√１１ｃｍ |
39高知県 | １ ８ ２ −３ ３ ２ａ×２ａ＝４ａ２ ４ ９ｘ２＋６ｘ＋１＋２ｘ２−６ｘ＝１１ｘ２＋１ ５ ２√３＋９√３/（√３√３）＝５√３ 〜 おまけ ［２］ 〜 １ ２×５×（−２）＋（−２）２＝−２０＋４＝−１６ ２ ｘ２−４ｘ−１２＝０ （ｘ−６）（ｘ＋２）＝０ より，大きい方はｘ＝６ ３ ３６π÷４＝３２π（半径３，高さ４の円柱） 表面積＝底面積×２＋側面積 ＝３２π×２＋４×６π＝１８π＋２４π＝４２πｃｍ２ ４ ∠Ｃ＝ｘ/２だから， ｘ＋２０＝ｘ/２＋５４ ｘ/２＝３４より，ｘ＝６８° |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36香川県 | １ −６＋１０＝４ ２ （−２）２−３×（−２）＝４＋６＝１０
２×３−ａ＝４（ａ−３）−７ ６−ａ＝４ａ−１２−７ −５ａ＝−２５より，ａ＝５ ６ ３（ｘ２−２ｘｙ−１５ｙ２） ＝３（ｘ−５ｙ）（ｘ＋３ｙ） ７ √５６√ｎ＝２√１４√ｎより，ｎ＝１４ ８ △ＡＢＥは二等辺三角形だから， ∠ＡＥＢ＝（１８０−５０）÷２＝６５ ∠ＡＥＤ＝１８０−６５＝１１５° |
40福岡県 | １ ７−８＝−１ ２ ３ａ＋１５−ａ＋２＝２ａ＋１７ ３ （−１）２＋４×（−１）＝１−４＝−３ ４ ３√２＋４√２＝７√２ ５ ５ｘ−２ｘ＝６＋７より，ｘ＝４ ６ （ｘ−４）（ｘ＋２）＝０より，ｘ＝４，−２ ７ ｙ＝ａｘ２に（５，７５）を代入すると， ７５＝２５ａより，ａ＝３ ｙ＝３ｘ２にｘ＝−２を代入して， ｙ＝３×（−２）２＝１２ ８ 積が４となるのは，１×４，２×２，４×１の３通り よって，３/３６＝１/１２ ９ ∠ＡＥＤ＝∠Ａ＋∠Ｂ＝∠Ａ＋∠Ｄ ＝６３＋２５＝８８° |
