|
正 答 6 | |||
| 41 佐賀県 〜 47 沖縄県 |
|
正 答 6 | |||
| 41 佐賀県 〜 47 沖縄県 |
| 41佐賀県 | 1 ア 2 イ 3x−4y−2x+6y=x+2y
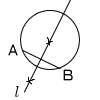 2 y(x2−4)=y(x+2)(x−2) 3 y=ax2 に(2,−8)を代入すると, −8=a×22 より,a=−2 y=−2x2にx=3を代入して,y=−8 4 150円以下になるのは, 3枚とも裏になる以外の7通り よって,7/8(8分の7) 5 右図参照 円周上に適当な2点A,Bをとり,その弦ABの垂直二等分線を作図すればよい (注)中心そのものを見つける必要はないので,1本でよい |
45宮崎県 | 1 −10
4 (x+3)(x+4)=0より,x=−3,−4 5 x=1のとき,y=2×12=2 x=3のとき,y=2×32=18
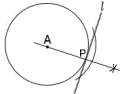 6 ∠B=∠A=40°(円周角)より, 6 ∠B=∠A=40°(円周角)より,x=90−40=50° 7 点Aより 次に,点Aを中心に,半径APの円を作図すればよい。 |
||||||||||||||||||||||||||||||||||||
| 42長崎県 | 1 7−15=−8
4 6a−3−2a−6=4a−9 5 2×3−(−2)2=6−4=2 6 (x−4)(x+3) 7 x(x+5)=0より,x=0,−5 [誤答例] 両辺を x で割って,x+5=0 x=−5(誤答) 8 x=1のとき,y=12=1 x=3のとき,y=32=9 したがって,
|
46鹿児島県 | 1 (1) 4+6=10
3 600×0.8×1.05=504円 4 a=xyより,a=24だから,y=24/x これにx=8を代入して,y=3 5 ∠D=∠A=50°(弧BCの円周角) また,∠ACB=90°(直径の円周角) よって,∠x=180−50−90=40° |
||||||||||||||||||||||||||||||||||||
| 43大分県 | 1 (1) −3 (2) 3x+y (3) x2+2x+2+x2−x−6=2x2+x−5
 3 −4y=−2x+3 3 −4y=−2x+3
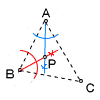
(大,小)=(4,2)(5,2)(6,3)の3通り よって,3/36=1/12(12分の1) 5 3点から等距離ということは,△ABCの内心(内角の二等分線の交点)を作図すればよい。 ∠Aの二等分線(青)と∠Bの二等分線(赤)を作図し,その交点をPとする。 |
47沖縄県 | 1 −5 2 4/10+5/10=9/10 3 −4 4 a2×2a=2a3 5 2x+2y−x+y=x+3y 6 2√2+3√2=5√2 〜 おまけ [2] 〜 1 4x=2×8より,x=4 2 −2y=−x−2
4 上式+下式より,4x=12となって,x=3,y=1 5 n=1,6,9の 3個 6 2x=10+4より,x=7 7 (x−4)2 8 (x−4)2=7より,x−4=±√7 x=4±√7 |
||||||||||||||||||||||||||||||||||||
| 44熊本県 | 1 0.11 2 6+14=20
5 √6+3√6=4√6 〜 おまけ [2] 〜 1 7x=−7より, x=−1 2 上式×5−下式より,−23y=46 x=3,y=−2 3 移項して,x2+4x=0 x(x+4)=0より,x=0,−4 4 10π×105/360=3πxm |
〜 おまけ [2] 〜 1 4x=16より,x=4 2 −2y=−x−2より,両辺を−2で割って
4 上式+下式より解いて,x=3,y=1 5 n=1,6,9で,3(個) 6 2x=14より,x=7 7 (x−4)2 8 (x−4)2=7より, x−4=±√7 x=4±√7 |