|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
| 25滋賀県 | 1 (1) 4−7=ー3 (2) 5a−10b+9b=5a−b
2 上式×2+下式×3より,7x=−14 x=−2,y=3 3 x2−6x−7=0 (x−7)(x+1)=0より,x=7,−1 4 y=ax2に値値を代入して,1=a×22 a=1/4となるから,y=1/4x2 これにx=−3を代入すると,y=1/4×(−3)2=9/4 5 (1) 45÷2=22.5° (2) ∠BAD=45°より,∠AEB=22.5° よって,AE=AB=4 また,AD=2√2 DE2=42+(2√2)2=24で,DE=√24=2√6cm 6 (1) 4 (2) x=b/a が整数になるのは14通り
|
29奈良県 | 1 (1) −35 (2) x+12x+2y=13x+2y (3) 8a+1 (4) 4√2−√2=3√2 2 0.7−(−1.8)=2.5°C 3 (1) 上式+下式より,3x=15 よって,x=5,y=3 (2) x2−7x+6=2x−8 x2−7x+6−2x+8=0 x2−9x+14=0 (x−2)(x−7)=0より,x=2,7 4 50−3a (個) 5 表面積=底面積(円)+側面積(おうぎ形) =42π+12×8π×6=16π+24π 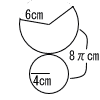 =40πcm2 =40πcm2 |
||||||||||||||||||||||||||||||||||
| 26京都府 | 1 −36÷4+4=−5 2 4a−2b−3a=a−2b 3 2√5−4√5=−2√5 4 y=a/xに代入して,a=9 y=9/xにx=6を代入して, y=9/6=3/2(1.5) 5 上式+下式×2より計算して,x=4,y=1 6 (x−3)(x−4)=0より, x=3,4 |
30和歌山県 | 1 (1) −2 (2) 9/12−10/12=−1/12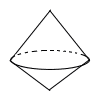 (3) 4x−3y (4) √3 (3) 4x−3y (4) √3(5) x2−4y2+4y2=x2 2 移項して,x2−3x−4=0 (x−4)(x+1)=より, x=4,−1 3 周=弦+弧=a×2+2a×π÷2 =2a+aπ(cm) 4 右図 |
||||||||||||||||||||||||||||||||||
| 27大阪府 | 1 −15 2 7x+5y 3 6x−15=4x+1 6x−4x=1+15 より, x=8 4 3√3+6√3=9√3 5 (x−4)2 6 取り出し方は全部で6通り このうち 0+2 と 1+3 が偶数になるから,
7 (1)エ (2) |
31鳥取県 | 1 −4−12=−16 2 4x+y
5 x2+x−6=0,(x+3)(x−2)=0,x=−3,2 6 10円玉x枚,5円玉y枚とすると,
10円玉が200枚,5円玉が250枚
8 ウ 9 ・PM=PM,または PMは共通 ・AM=BM ・∠PMA=∠PMB=90° ・2辺とその間の角がそれぞれ等しいから ・△PAM≡△PBM |
||||||||||||||||||||||||||||||||||
| 28兵庫県 | 1 7 2 3/6−4/6=−1/6 3 −3a 4 ∠D=70°だから,∠x=110−70=40° 5 y=a/xに値を代入して,4=a/8より a=32 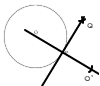 y=32./x (x分の32) y=32./x (x分の32)6 (x+6)(x−1)=0より,x=−6,1 7 1 OPを結んで延長する 2 点Pを中心にOの対称点O’をとる 3 OとO’から弧をかいて,交点Qをとる 4 PとQを結べば接線ができあがる |
32島根県 | 1 9−2=7 2 2√2+4√2=6√2 3 −2x+2y+5x+5y−5=3x+7y−5 4 (x−2)(x−3)=0より,x=2,3 5 (A奇数+B偶数)+(A偶数+B奇数) =2/3×1/3+1/3×2/3=4/9 6 50°を分割するように補助線を考えればよい ∠x=50−15=35(°) 7 △PQR∽△CBR(相似比1:2)だから, 4:BR=1:2より,BR=8(cm) 8 6×4π=24π(cm2) 9 y=a/xに値を代入してa=8より,(y=)8/x 10 平行でなく,交わらない辺だから,CF |