（８） 平行四辺形の性質２ 学習日　 　 月　 　日（　　）
［平行四辺形の定義］
　2組の対辺がそれぞれ
　　平行な四角形		 ［性質１］
　2組の対辺は
　　それぞれ等しい		 ［性質２］
　2組の対角は
　　それぞれ等しい		 ［性質３］
　対角線はそれぞれの
　　中点で交わる。
印刷して、紙の上でやってネ！　　印刷用
空欄をうめて,次のことがらを証明しなさい。　　　　　　　
１ 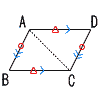［性質1］平行四辺形の2組の対辺は,それぞれ等しい

［証明１］
△ABCと　　　　　において,
　 AC ＝　　　　（　　　　）
∠BAC ＝　　　　（AB//DC,錯角）
∠BCA ＝　　　　（BC//AD,錯角）

合同条件：
　(　　　　　　　　　　　　　)
　　　　　がそれぞれ等しいから,

△ABC≡
　よって, AB＝　　　　, BC＝　		 ２ 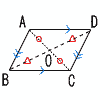［性質3］平行四辺形の対角線は,それぞれの中点で交わる

［証明３］
△ABOと　　　　　において,
　 AB ＝　　　（証明１より）
∠OAB ＝　　　（AB//DC,錯角）
∠OBA ＝　　　（AB//DC,錯角）

合同条件：
　(　　　　　　　　　　　)
　　　　　　がそれぞれ等しいから,

△ABO≡
　よって, OA＝　　　　, OB＝　
３ 　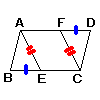ABCDの辺上に,BE＝DFとなる点ＥとＦをとるとき,AE＝CF

［証明］
△ABEと　　　　　において,
　 AB ＝　　　（平行四辺形の対辺）
BE ＝　　　（仮　　定）
∠B ＝　　　（平行四辺形の対角）

合同条件：
　(　　　　　　　　　　　)
　　　　　がそれぞれ等しいから,

△ABE≡　　　　で, AE＝		 ４ 　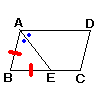ABCDで,∠Aの二等分線を引き,辺BCとの交点をＥとするとき,△ABEは二等辺三角形となる

［証明］
△ABEにおいて,
　 ∠BAE ＝　　　（仮　　定）
∠BEA ＝　　　（AD//BC,錯角）

よって, ∠BAE＝∠BEA
　　　　　　　　が等しいから,

　△ABEは
各図で,青印は仮定,赤印は結論 を表している

［トップに戻る］ ［前ページに戻る］ ［次ペ−ジに進む］ ［答のペ−ジに進む］