|
���@���@�U | |||
| 41�@���ꌧ�@�`�@47�@���ꌧ |
|
���@���@�U | |||
| 41�@���ꌧ�@�`�@47�@���ꌧ |
| 41���ꌧ | �P (1) 3�{5��8 �@(2) �Qx�{6y�|10x�|5y���|8x�{y �@(3) �|(18/12)x���| �@(4) (��5)2�|(��2)2��5�|2��3 �Q xy(x�|6) �R ���̌������,
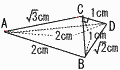 �S (�E�}�Q��) �S (�E�}�Q��)�@3�ӂ̔���,��ABC����ACD�� �@�@���p�O�p�`��,���_C�̉�肪 �@�@���ׂ�90���̎O�p���ɂȂ� �@�̐ρ� �@�@�� 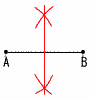 �T �E�} �T �E�}�@�EA��B�𒆐S�ɒ���AB�̌ʂ����� �@�E�ʂ̌�_�ǂ������Ō��� �U ��BAC��95�|64��31�� �@����ĉ~���p���,��BDC����BAC��31�� �V �@�@�C �@�@ �Z�c�ŕp�l��120�`150���̊K�� �@�A �~�cQ1��10.5�l�ڂ�,60�`90���̊K�� �@�B �~�c�ݐϓx����,3�{9�{7��19�l �@�C �Z�c�͈́�210�|30��180�� |
44�F�{�� |
�R 7x�{4y�|8x�{5y���|x�{9y
�T 42�|12x�{9�{12x�{10��4x2�{19 �U ��10�{2��10��3��10 �@�@�@�Q�Ԗ��̈ꕔ�@�`���܂��` �P �ڍ�����,�|x���| 9���, x��9 �Q �^����2(x2�|9)��2(x�{3)(x�|3) 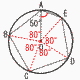 �R ��AOE��360�|80�~4��40�� �@�����,��OAE��(180�|40)��2��70�� �S �Ea�{b��6�̂Ƃ�, (a,b)��(3,3) �Ea�{b��8�̂Ƃ�, (a,b)��(3,5) (4,4) (5,3) �Ea�{b��12�̂Ƃ�, (a,b)��(5,7) (6,6) (7,5) �@�S����7�ʂ肾����, �m����7��52��7/25 |
|||||||||||||||||||||||||||||||||||||||||||||||
| 42���茧 | �@�@�y�@A�@�z �P 1�{2�~9��19 �Q 2250�~0.9��2025�~ �R 3��2�|2��2����2
�T �㎮�~2�{�������,7x��7��,x��1 �@������㎮�ɑ������,2�{y��4��,y��2 �@�@�����, x��1, y��2 �U (a�|2)(a�|3) �V ���̌������,
 �@CG, DH, EH, FG��,�@4�{ �@CG, DH, EH, FG��,�@4�{�X 105���s����2���������, �@��x��105�|42��63�� 10 �E�} �@�@�y�@B�@�z
�R 2250�~0.9��2025�~
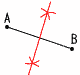
�@(x,y)��(-15,-1) (-5,-3) (-3,-5) (-1,-15) (1,15) �@�@(3,5) (5,3) (15,1) ��, 8�� �T �����~6���,3x�|(y�{2)���|10 �@���������,3x�|y���|8 �@����ɏ㎮��������,5x���|5��,x���|1 �@������㎮�ɑ�������,�|2�{y��3 �@�@�����, x���|1, y��5 �U (a�{1)(a�|5) �V x�{1���}��3���, x���|1�}��3 �W BH����52�{42�{32����25�{16�{9��5��2cm  �X ��x��42�|20��22�� �X ��x��42�|20��22��10 �E�} �@�EAB�a�Ƃ���~������ �@�EAB�̐��������Ƃ̌�_���Ƃ� |
45�{�茧 | �P 3�|7���|4
�S �㎮�~2�{�����~7���,8x�{21x���|4�{91 �@�@29x��87��,x��3 �@������㎮�ɑ������, 4�~3�{7y���|2�� ,y���|2 �@�����, x��3,y���|2 �T �^����(���|2��)2��(15�|2�~6)2��32��9 �U �A �@�@�@�A�c5/36�@�@�C�c4/36 �V �x�����z���p�`�̌`���قړ�����, �@2024�N����2�������E�ɂ���Ă��邩��B 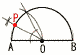 �W �E�}(���S�p30��) �W �E�}(���S�p30��)�E�`�𒆐S��,��OC������(��AOC�͐��O�p�`) �E��AOC�̓���l ������ �E�~O�̉~����l �Ƃ̌�_P���Ƃ� |
|||||||||||||||||||||||||||||||||||||||||||||||
| 46�������� | �P (1) 7�{6��13
�@(4) 60��22�~3�~5�@84��22�~3�~7��� �@�@�ŏ����{����22�~3�~5�~7��420 �@(5) �t����, �A �@�@�����, �A �G �Q ���̌������,
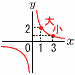 �S (�E�}�Q��) �S (�E�}�Q��) �@x��3�̂Ƃ�, �ŏ��ly��2/3�� �@x��1�̂Ƃ�, �ő�ly��2/1��2 �@�����, �T 37�b��37/60��������,
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| 43�啪�� | �P (1) 3�@�@(2) (�|8)��(�|4)��2
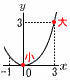 �R (�E�}�Q��) �R (�E�}�Q��)�@x��0�̂Ƃ�, �ŏ��ly�� �@x��3�̂Ƃ�, �ő�ly�� �@�����, 0��y��3 �S (�E�}�Q��) �@��DAF��,��F�̊O�p��36�{45�c�A 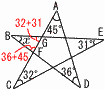 �@��CEG��,��G�̊O�p��32�{31�c�C �@��CEG��,��G�̊O�p��32�{31�c�C�@�A�{�C���,��BFG��, �@�@��x��180�|(81�{63)��36�� �T �D���Ȑ��k��x�l�Ƃ����,
�U �E�} 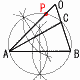 �@��AB�̉~���p�ƂȂ�悤�ȉ~ �@��AB�̉~���p�ƂȂ�悤�ȉ~�@�@�܂�,��ABC�̊O�ډ~�������悢 �@�E��AB�̐��������������c�A �@�E��AC�̐��������������c�C �@�E�A�ƃC�̌�_�𒆐S�Ƃ���O�ډ~������ �@�E�O�ډ~�ƕ�OA�̌�_���o�Ƃ��� |
47���ꌧ | �P �|7 �Q �|10�~ �R 4.1�|2.3��1.8 �S 3��3 �T 3a�~4b2��12ab2 �U �|5x�{y�{2x�{4y���|3x�{5y �@�@�@�Q�Ԗ��̈ꕔ�@�`���܂��` �P 5x�|3x��4�{2���, x��3 �Q �㎮�{�����~2���,5x��10��,x��2 �@����������ɑ������,2�|y��6��,y���|4 �@�����, x��2,y���|4 �R x2�|4y2 �S ax(3x�|2) �T ���̌������,
�V ��x��40�{23��63�� �W ���������ɕ��ׂ��, 4 4 5�b7 8 9 �@�����l��(5�{7)��2��6m �X �s�Ǖi��x�Ƃ����,
|
|||||||||||||||||||||||||||||||||||||||||||||||
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n |