|
���@���@�U | |||
| 41�@���ꌧ�@�`�@47�@���ꌧ |
|
���@���@�U | |||
| 41�@���ꌧ�@�`�@47�@���ꌧ |
| 41���ꌧ | �P (1) �|7 �@�@(2) 8x�{4y�|3x�{9y��5x�{13y �@�@(3) 3y2 �@�@(4) 3��3�|2��3����3 �Q (x�|8)(x�{5) �R ���̌������, 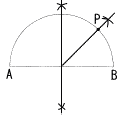
�̐ρ� �@��21��cm3 �T �E��} �E���S�p��4�������� 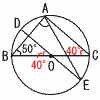 �U (�E�}�Q��) �U (�E�}�Q��)BC�����a������, �@��BAC��90����,��C��40�� ��DOB��40��(���p) ��BOE��180�|40��140�� �����,��BAE��140��2��70�� �V �A,�I |
44�F�{�� | �P 0.2�@�@�Q 7�|20���|13
�@�@�@�Q�Ԗ��̈ꕔ�@�`���܂��` �P 5x�{x��6�|18 �@�@6x���|12��, x���|2 �Q ���̌������,
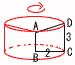
�̐ρ�(�~��)�|(����1�̉~��) �@�@��32���~3�| �S �S���̎��o������3�~5��15�ʂ� 6�_��(A,6),(B,3)�@12�_��(B,6),(C,5) �@�����, �m����4/15 |
|||||||||||||||||||||||||||||||||||
| 42���茧 | �@�@�y�@�O���@�z �P 3�{16��19 �Q 5�|2��5�{1�{2��5��6 �R 12a�{8b�|6a�|21b��6a�|13b �S ���̌������, 
�@�m����6/36�� 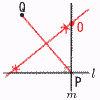 �U �B
�U �By�ɂ��ĉ�����,y���| �@���_��ʂ�,�X���| �V�@�E�} �E����PQ�̐��������� �@�@����m�Ƃ̌�_���Ƃ�,O�Ƃ��� �W (�E���Q��) �O�p�� 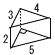 �@���́�( �@���́�(�@�@�y�@����@�z �P 3�{1��4 �Q 4��3�{��3��5��3 �R (5�|3a)km �S �㎮�~2�{�������,7x��7��,x��1 �@������㎮�ɑ������,2�|y��5��,y���|3 �@�����, x��1,y���|3 �T (x�|4)(x�{1)��0���, x��4,�|1 �U ������̑�����x�{�Ƃ����,
�V 2024��23�~11�~23��22�~23�~4 
�@��x��360�|108�~2��144�� �X 32���~5��45��cm3 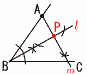 10 �E�} 10 �E�}�E��B�̓���l ������ �EA����l �ɐ���m�����낷 �El ��m�̌�_��P�Ƃ��� |
45�{�茧 |
�S �^����2a�|4b�|5a�{4b���|3a �@�@���|3�~(�|5)��15 �T (x�{6)(x�|2)��0���, x���|6,2 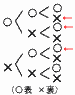 �U �E�̎��`�}���, �U �E�̎��`�}���, �V �G �W ���} 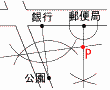 �E�X�ǂ��璼�����H�̐��������낷 �E��s�ƌ��������Ԑ����̐������������� �E2�����̌�_��P |
|||||||||||||||||||||||||||||||||||
| 46�������� | �P (1) 41�|35��6 �@(2)
�@(4) 72��8�~32���, 8,24,72 �@(5) �C,�G �Q a(x�|y)�|b(x�|y)��(a�|b)(x�|y) �R 1.1x��176���, x��176��1.1��160�~  �S (�E�}�Q��) �S (�E�}�Q��) ��P��90�|y��69�� ��x��180�|(60�{69) �@��180�|129��51�� �T �ԋʂ�x�Ƃ����,
�@x��900�� |
|||||||||||||||||||||||||||||||||||||
| 43�啪�� | �P (1) �|4�@�@(2) �|16��8�|�|2 �@(3) 4x�|7�|4�|x��3x�|11
�Q ���̌������,
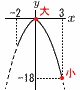
�@x��3�̂Ƃ�, �@�@�ŏ��ly���|2�~32���|18 �@x��0�̂Ƃ�,�ő�ly��0 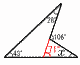 �@�����, �|18��y��0 �@�����, �|18��y��0�S (�E�}�Q��) �@��x��106�|(28�{43) �@�@��106�|71��35�� �T (�E�}�Q��)�@�A,�E 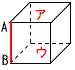 �U ���} �U ���}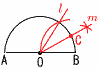 ��COB��30���ƂȂ�悢 �E1��OB�̐��O�p�`����,l ������ �E60���̓���m������ �E |
47���ꌧ | �P �|5 �Q 9�~(�| �R 3�{3��6 �S ��3�~2��3�E��2��6��2 �T 4a2�~5a3��20a5 �U 10x�|5y�|6x�{2y��4x�|3y �@�@�@�Q�Ԗ��̈ꕔ�@�`���܂��` �P 5x�|4x���|6�|3���, x���|9 �Q �㎮�{�����~3���,7x��7��,x��1 �@������㎮�ɑ������,1�{3y���|5��,y���|2 �@�����, x��1,y���|2 �R x2�|6xy�{9y2 �S (x�{5)(x�|5) �T ���̌������,
|
|||||||||||||||||||||||||||||||||||
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n |