|
(29)奈良県 | 学習日 月 日( ) |
| 1 | (1) | 5 | 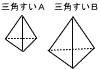 図の2つの三角すいA,Bは相似であり,その相似比は2: 3である。三角すいAの体積が24cm3であるとき,三角すいBの体積を求めよ。 図の2つの三角すいA,Bは相似であり,その相似比は2: 3である。三角すいAの体積が24cm3であるとき,三角すいBの体積を求めよ。 |
|||||||
| (2) | ||||||||||
| (3) | (x+2)(x-5)-2(x-1) |
6 | 硬貨を3回投げて移動した結果,点Pが原点Oにある確率を求めよ。 |
|||||||
| (4) | √2×√6-√27 |
|||||||||
| 2 |
|
7 | 図のように,3点A,B,Cがある。次の条件①,②を満たす点Pを,定規とコンパスを使って解答欄の枠内に作図せよ。なお,作図に使った線は消さずに残しておくこと。
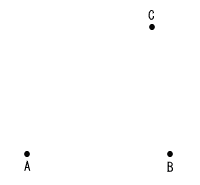 |
|||||||
| 3 | 2次方程式 x2+5x+1=0 を解け。 |
|||||||||
| 4 | a<0, b<0のとき, a+b, a-b, ab, |
|||||||||
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |